
| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 把已知等式的左边第一项利用两角和的正弦公式及特殊角的三角函数值化简,与第二项合并后,
利用特殊角的三角函数值及两角差的余弦公式化简,即可求出答案.
解答 解:∵sin(α+$\frac{π}{6}}$)+cosα=-$\frac{{\sqrt{3}}}{3}$,
∴sinαcos$\frac{π}{6}$+cosαsin$\frac{π}{6}$+cosα=-$\frac{\sqrt{3}}{3}$,
即$\frac{\sqrt{3}}{2}$sinα+$\frac{3}{2}$cosα=-$\frac{\sqrt{3}}{3}$,
∴$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα=-$\frac{1}{3}$,
即cos($\frac{π}{6}$-α)=-$\frac{1}{3}$.
故选:C.
点评 本题考查了两角和与差的正弦、余弦函数公式,以及特殊角的三角函数值的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
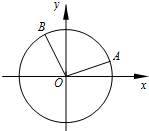 如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点A,B.若点A的横坐标是$\frac{3\sqrt{10}}{10}$,点B的纵坐标是$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点A,B.若点A的横坐标是$\frac{3\sqrt{10}}{10}$,点B的纵坐标是$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com