
分析 利用两个向量坐标形式的运算法则求得$\overrightarrow{a}$-$\overrightarrow{b}$ 的坐标,再利用向量的模的定义,求得|$\overrightarrow{a}$-$\overrightarrow{b}$|的值.
解答 解:∵已知$\overrightarrow{a}$=(cos$\frac{π}{6}$,sin$\frac{π}{6}$)=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),$\overrightarrow{b}$=(cos$\frac{5π}{6}$,sin$\frac{5π}{6}$)=(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),∴$\overrightarrow{a}$-$\overrightarrow{b}$=($\sqrt{3}$,0),
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(\sqrt{3})}^{2}{+0}^{2}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查两个向量坐标形式的运算,向量的模的定义,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (1,+∞) | C. | ($-\frac{1}{2}$,0)∪(2,+∞) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
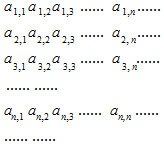 如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )
如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )| A. | d+q1+q2=a2,5 | |
| B. | a2,1+a2,3+a2,5+…+a2,21=$\frac{441}{2}$ | |
| C. | a1,2+a3,2+a5,2+…+a21,2=411-1 | |
| D. | ai,j=$\left\{\begin{array}{l}(2j-1){2^{1-i}},j为正奇数\\(2j-1){2^{i-1}},j为正偶数\end{array}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com