某考生参加一所大学自主招生考试,面试时从一道数学题,两道自然科学类题,三道社科类题中任选两道回答,且该生答对每一道数学、自然科学、社科类试题的概率依次为0.6、0.7、0.8.
(1)求该考生恰好抽到两道社科类试题的概率;
(2)求该考生抽到的两道题属于不同学科类并且都答对的概率.
解:(1)由题意知本题是一个古典概型,
试验发生包含的事件是从6道题目中选2道,共有C
62=15,
满足条件的事件是考生恰好抽到两道社科类试题,共有3种结果,
∴P=
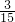
=

.
(2)该考生抽到一道数学题,一道自然科学类题的概率为P
1=

;
该考生抽到一道数学题,一道社科类试题的概率为P
2=
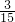
;
该考生抽到一道自然科学类题,一道社科类试题的概率为P
3=
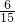
.
∴该考生抽到的两道题属于不同学科类并且都答对的概率为
P=

×0.6×0.7+
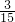
×0.6×0.8+
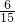
×0.7×0.8=0.376.
分析:(1)本题是一个古典概型,试验发生包含的事件是从6道题目中选2道,满足条件的事件是考生恰好抽到两道社科类试题,写出结果数,根据古典概型概率公式得到结果.
(2)先做出考生抽到一道数学题,一道自然科学类题的概率,抽到一道数学题,一道社科类试题的概率,抽到一道自然科学类题,一道社科类试题的概率,根据答对的概率,得到结果.
点评:本题考查相互独立事件同时发生的概率,考查古典概型的概率公式,是一个比较简单的综合题目,注意本题出现的数字比较多,要分析清楚.

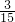 =
= .
. ;
;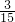 ;
;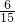 .
. ×0.6×0.7+
×0.6×0.7+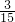 ×0.6×0.8+
×0.6×0.8+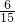 ×0.7×0.8=0.376.
×0.7×0.8=0.376.

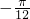




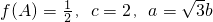 ,求△ABC的面积.
,求△ABC的面积.