
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的最大值;
的最大值;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)根据函数单调性可将问题转化为![]() 在
在![]() 上恒成立问题,通过分离变量的方式将问题转化为
上恒成立问题,通过分离变量的方式将问题转化为![]() ,利用导数求得
,利用导数求得![]() 的最大值,进而得到结果;
的最大值,进而得到结果;
(2)将问题转化为![]() 的证明;利用
的证明;利用![]() 单调递增和零点存在定理可确定存在
单调递增和零点存在定理可确定存在![]() ,使得
,使得![]() ,从而得到
,从而得到![]() ;根据导函数正负可确定
;根据导函数正负可确定![]() 单调性,进而得到
单调性,进而得到![]() ,化简后,结合基本不等式可证得结论.
,化简后,结合基本不等式可证得结论.
由函数解析式可知,![]() 定义域为
定义域为![]() .
.
(1)![]() ,
,
![]() 在
在![]() 上是减函数,
上是减函数,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立
恒成立
令![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,解得:
,解得:![]() ,
,
![]() 的最大值为
的最大值为![]() .
.
(2)由(1)知:![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]() ,
,
![]() 由零点存在定理可知,存在
由零点存在定理可知,存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
![]() .
.
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增,
单调递增,
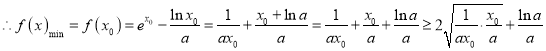
![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时取等号).
时取等号).
![]() 当
当![]() 时,
时,![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
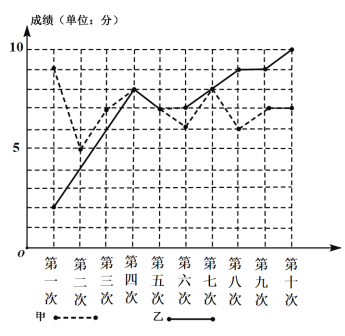
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 、
、![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]()
![]() 的四个顶点围成的四边形面积为
的四个顶点围成的四边形面积为![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的短轴端点.
的短轴端点.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过椭圆
过椭圆![]() 的右焦点作互相垂直的两条直线分别与椭圆
的右焦点作互相垂直的两条直线分别与椭圆![]() 相交于
相交于![]() ,
,![]() 和
和![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=0,![]() (n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
(n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
A.![]() 是单调递增数列,
是单调递增数列,![]() 是单调递减数列B.
是单调递减数列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )
A.3233万元B.4706万元C.4709万元D.4808万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
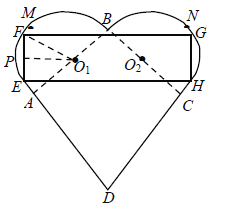
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com