
分析 由xk+1=xk2+xk(k∈N*),可得:$\frac{1}{{x}_{k}+1}$=$\frac{1}{{x}_{k}}-\frac{1}{{x}_{k+1}}$.于是$\frac{1}{{x}_{1}+1}$+$\frac{1}{{x}_{2}+1}$+…+$\frac{1}{{x}_{100}+1}$=2-$\frac{1}{{x}_{101}}$,另一方面:x1=$\frac{1}{2}$,xk+1=xk2+xk(k∈N*),可得xn+1=xn(xn+1)>xn>1,(n≥2).进而得出答案.
解答 解:∵xk+1=xk2+xk(k∈N*),∴$\frac{1}{{x}_{k}+1}$=$\frac{1}{{x}_{k}}-\frac{1}{{x}_{k+1}}$.
∴$\frac{1}{{x}_{1}+1}$+$\frac{1}{{x}_{2}+1}$+…+$\frac{1}{{x}_{100}+1}$=$(\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}})$+$(\frac{1}{{x}_{2}}-\frac{1}{{x}_{3}})$+…+$(\frac{1}{{x}_{100}}-\frac{1}{{x}_{101}})$=2-$\frac{1}{{x}_{101}}$
则[$\frac{1}{{x}_{1}+1}$+$\frac{1}{{x}_{2}+1}$+…+$\frac{1}{{x}_{100}+1}$]=$[2-\frac{1}{{x}_{101}}]$,
∵x1=$\frac{1}{2}$,xk+1=xk2+xk(k∈N*),∴xn+1=xn(xn+1)>xn>1,(n≥2).
因此数列{xn}单调递增,∴$\frac{1}{{x}_{101}}$∈(0,1).
∴$[2-\frac{1}{{x}_{101}}]$=1,
故答案为:1.
点评 本题考查了递推关系、“裂项求和”方法、取整函数的性质,考查了推理能力与计算能力,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
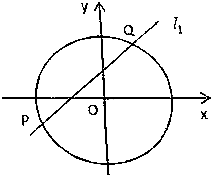 如图所示:已知直线l1:y=kx+1与圆C:x2+y2=4相交于P、Q两点.
如图所示:已知直线l1:y=kx+1与圆C:x2+y2=4相交于P、Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 102 | B. | 103 | C. | 104 | D. | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 24 | C. | 23 | D. | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com