练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（1+m，1-m），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数m的值为-3．

    分析 根据$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），$\overrightarrow{a}$∥$\overrightarrow{b}$，则x1y2-x2y1=0，建立等式关系，解之即可求出所求．

    解答 解：∵$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（1+m，1-m），$\overrightarrow{a}$∥$\overrightarrow{b}$，
    ∴x1y2-x2y1=0，即：1×（1-m）-（-2）×（1+m）=0，
    解得：m=-3，
    故答案为：-3．

    点评 本题主要考查了平面向量共线（平行）的坐标表示，解题的关键是平行向量的充要条件，属于基础题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．a＞0且a≠$\frac{1}{2}$，求g（x）=lnx-ax-$\frac{a-1}{x}$在区间[1，+∞）上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知{an}是等比数列，{bn}是等差数列，且a1=b1=1，a1+a2=b4，b1+b2=a2．
    （1）求{an}与{bn}的通项公式；
    （2）记数列{an+bn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知角α的顶点在坐标原点，始边在x轴的非负半轴上，终边上有一点P（-2，1），则sinα的值为（　　）
    A．$\frac{\sqrt{5}}{5}$B．-$\frac{\sqrt{5}}{5}$C．$\frac{2\sqrt{5}}{5}$D．-$\frac{2\sqrt{5}}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知sin（α+$\frac{7π}{6}$）=1，则cos（2α-$\frac{2π}{3}$）的值是（　　）
    A．0B．1C．-1D．1或-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

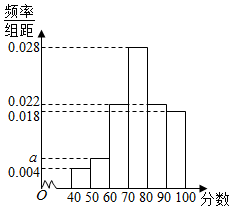    4．如图是根据某班50名同学在某次数学测验中的成绩（百分制）绘制的概率分布直方图，其中成绩分组区间为：[40，50），[50，60），…，[80，90），[90，100]．
    （1）求图中a的值；
    （2）计算该班本次的数学测验成绩不低于80分的学生的人数；
    （3）根据频率分布直方图，估计该班本次数学测验成绩的平均数与中位数（要求中位数的估计值精确到0.1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．《九章算术》是中国古代数学名著，其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致．如某一问题：现有扇形田，下周长（弧长）20步，径长（两段半径的和）24步，则该扇形田的面积为120平方步．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．随机抽取高一年级n名学生，测得他们的身高分别是a1，a2，…，an，则如图所示的程序框图输出的s=$\frac{{{a_1}-{a_2}+…+{{（-1）}^{n+1}}{a_n}}}{n}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若sin（α-$\frac{π}{3}$）=$\frac{4}{5}$，则cos（2α+$\frac{π}{3}$）=$\frac{7}{25}$．

    查看答案和解析>>

    同步练习册答案