
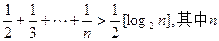 为大于2的整数,
为大于2的整数,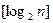 表示不超过
表示不超过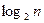 的最大整数. 设数列
的最大整数. 设数列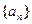 的各项为正,且满足
的各项为正,且满足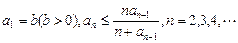
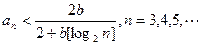
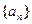 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);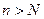 时,对任意b>0,都有
时,对任意b>0,都有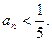 .
. 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:不详 题型:填空题
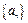 中,
中,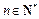 ,若
,若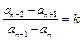 (
(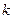 为常数),则称
为常数),则称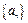 为“等差比数列”. 下列是对“等差比数列”的判断:
为“等差比数列”. 下列是对“等差比数列”的判断: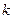 不可能为0 ②等差数列一定是等差比数列
不可能为0 ②等差数列一定是等差比数列 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 容影响了市容市貌. 今年该市决定引进一
容影响了市容市貌. 今年该市决定引进一 种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是
种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是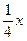 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经 过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满
过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满 足洗车净水需求)
足洗车净水需求)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
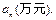
 与n的关系式;
与n的关系式;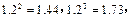
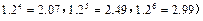
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com