
分析 利用分析法证明,即可得出结论.
解答 证明:要证明:${({{a^3}+{b^3}})^{\frac{1}{3}}}<{({{a^2}+{b^2}})^{\frac{1}{2}}}$,
只需要证明:(a3+b3)2<(a2+b2)3.
只需要证明:a6+b6+2a3b3<a6+b6+3a4b2+3a2b4,
只需要证明:2ab<3a2+3b2,
只需要证明:3(a-$\frac{1}{3}$b)2+$\frac{8}{3}$b2>0,
∵a>0,b>0,
∴3(a-$\frac{1}{3}$b)2+$\frac{8}{3}$b2>0.
∴原不等式成立.
点评 本题主要考查用分析法证明不等式,把证明不等式转化为寻找使不等式成立的充分条件,直到使不等式成立的充分条件显然已经具备为止.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,2) | B. | ($\frac{1}{3}$,2) | C. | ($\frac{2}{3}$,3) | D. | ($\frac{1}{3}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
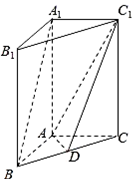 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com