
| 年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
分析 (Ⅰ)首先根据表格与公式求得相关数据,然后代入线性回归方程求得$\widehat{a}$,由此求得线性回归方程;
(Ⅱ)将先15代入(Ⅰ)中的回归方程即可求得张三同学15岁时的身高.
解答 解:(Ⅰ)由题意得$\overline{x}$=$\frac{1}{7}$(7+8+9+10+11+12+13)=10,
$\overline{y}$=$\frac{1}{7}$(121+128+135+141+148+154+160)=141,
$\sum_{i=1}^{7}$(${{(x}_{i}-\overline{x})}^{2}$=9+4+1+0+1+4+9=28,
$\sum_{i=1}^{7}$(xi-$\overline{x}$)(yi-$\overline{y}$)=(-3)×(-20)+(-2)×(-13)+(-1)×(-6)+0×0+1×7+2×13+3×19=182,
所以$\widehat{b}$=$\frac{182}{28}$=$\frac{13}{2}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=141-$\frac{13}{2}$×10=76,
所求回归方程为$\widehat{y}$=$\frac{13}{2}$x+76.
(Ⅱ)由(Ⅰ)知,$\widehat{b}$=$\frac{13}{2}$>0,
故张三同学7岁至13岁的身高每年都在增高,平均每年增高6.5cm.
将x=15代入(Ⅰ)中的回归方程,得$\widehat{y}$=$\frac{13}{2}$×15+76=173.5,
故预测张三同学15岁的身高为173.5cm.
点评 本题考查了求线性回归方程问题,考查计算能力,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,且P、Q不是正方体的顶点,则|PR|的最小值是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,且P、Q不是正方体的顶点,则|PR|的最小值是( )| A. | $\frac{{\sqrt{42}}}{6}$ | B. | $\frac{{\sqrt{30}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | 1 | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
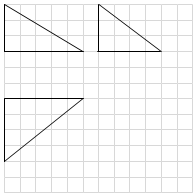 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )| A. | 25π | B. | 50π | C. | 75π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
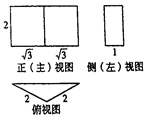
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com