
分析 根据三角函数的诱导公式,化简证明即可.
解答 证明:cos($\frac{5k-1}{5}$π-θ)+cos($\frac{5k+1}{5}$π+θ)
=cos(kπ-$\frac{π}{5}$-θ)+cos(kπ+$\frac{π}{5}$+θ)
=cos[kπ-($\frac{π}{5}$+θ)]+cos[kπ+($\frac{π}{5}$+θ)],
当k为偶数时,原式=cos[-($\frac{π}{5}$+θ)]+cos($\frac{π}{5}$+θ)=2cos($\frac{π}{5}$+θ);
当k为奇数时,原式=-cos($\frac{π}{5}$+θ)-cos($\frac{π}{5}$+θ)=-2cos($\frac{π}{5}$+θ);
综上,原式=(-1)k•2cos($\frac{π}{5}$+θ),(k∈Z),等式成立.
点评 本题考查了三角函数的诱导公式与分类讨论思想的应用问题,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
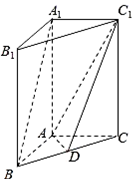 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
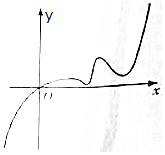 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | e | C. | 3 | D. | 2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com