
分析 (1)设|PF1|=m,|PF2|=n,运用椭圆的定义和余弦定理及三角形的面积公式,可得b,再由离心率公式和a,b,c的关系,求得a,进而得到椭圆方程;
(2)由题意可得MN的斜率存在,且不为0,设M(x1,y1),N(x2,y2),MN方程为x=my-4,代入椭圆方程,可得y的方程,由判别式大于0,韦达定理,再由S${\;}_{△MN{F}_{1}}$=|S${\;}_{△NT{F}_{1}}$-S${\;}_{△MT{F}_{1}}$|=$\frac{1}{2}$|TF1|•|y1-y2|,求得△MNF的面积,化简整理,运用基本不等式可得最大值.
解答 解:(1)根据椭圆的定义,设|PF1|=m,|PF2|=n,
则在△PF1F2中,根据余弦定理得,
cos60°=$\frac{{m}^{2}+{n}^{2}-4{c}^{2}}{2mn}$=$\frac{(m+n)^{2}-4{c}^{2}-2mn}{2mn}$
即$\frac{1}{2}$=$\frac{4{a}^{2}-4{c}^{2}-2mn}{2mn}$,
所以3mn=4a2-4c2=4b2;
又S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$mn•sin60°=$\frac{\sqrt{3}}{4}$mn=$\frac{\sqrt{3}}{4}$•$\frac{4}{3}$b2=$\frac{\sqrt{3}}{3}$b2=$\sqrt{3}$,
解得b2=3,
由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,又a2-b2=c2,
所以a=2.
所以椭圆的标准方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由题意可得MN的斜率存在,且不为0,
设M(x1,y1),N(x2,y2),MN方程为x=my-4,
代入椭圆方程,整理得(3m2+4)y2-24my+36=0,
则△=242m2-144(3m2+4)>0,所以m2>4.
y1+y2=$\frac{24m}{4+3{m}^{2}}$,y1y2=$\frac{36}{4+3{m}^{2}}$,
则△MNF1面积S${\;}_{△MN{F}_{1}}$=|S${\;}_{△NT{F}_{1}}$-S${\;}_{△MT{F}_{1}}$|=$\frac{1}{2}$|TF1|•|y1-y2|=$\frac{3}{2}$$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\frac{3}{2}$$\sqrt{(\frac{24m}{4+3{m}^{2}})^{2}-\frac{144}{4+3{m}^{2}}}$=18•$\frac{\sqrt{{m}^{2}-4}}{4+3{m}^{2}}$
=6•$\frac{1}{\frac{{m}^{2}-4+\frac{16}{3}}{\sqrt{{m}^{2}-4}}}$=6•$\frac{1}{\sqrt{{m}^{2}-4}+\frac{\frac{16}{3}}{\sqrt{{m}^{2}-4}}}$≤$\frac{6}{2\sqrt{\frac{16}{3}}}$=$\frac{3\sqrt{3}}{4}$.
当且仅当$\sqrt{{m}^{2}-4}$=$\frac{\frac{16}{3}}{\sqrt{{m}^{2}-4}}$即m2=$\frac{28}{3}$.(此时适合△>0的条件)取得等号.
则三角形MNF1面积的最大值是$\frac{3\sqrt{3}}{4}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和解三角形知识,考查直线和椭圆方程联立,运用韦达定理和判别式大于0,以及直线的斜率公式,考查基本不等式的运用:求最值,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{{\sqrt{35}}}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
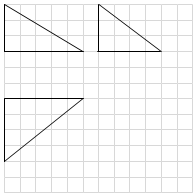 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )| A. | 25π | B. | 50π | C. | 75π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
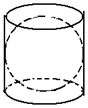 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )| A. | 2R | B. | $\frac{4R}{3}$ | C. | $\frac{2}{3}R$ | D. | $\frac{R}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com