
分析 利用平方关系,通过配方法对抛物线进行变形,消去参数即可得到顶点的轨迹.
解答 解:∵x2-2y-6xsinθ-9cos2θ+8cosθ+9=0,
∴2y=x2-6xsinθ-9(1-sin2θ)+8cosθ+9
∴y=$\frac{1}{2}$(x-3sinθ)2+4cosθ,
设该抛物线的顶点为(x,y),则x=3sinθ,y=4cosθ,
消去参数θ,得$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1,
即顶点的轨迹是椭圆.
故答案为:椭圆.
点评 本题考查参数方程、平方关系、配方法、椭圆方程、抛物线方程,注意解题方法的积累,利用平方关系对表达式进行变形是解题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
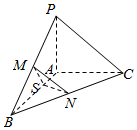 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB=2,S为AB上一点,且AB=4AS,M,N分别为PB,BC的中点,则点C到平面MSN的距离为$\sqrt{3}$.
在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB=2,S为AB上一点,且AB=4AS,M,N分别为PB,BC的中点,则点C到平面MSN的距离为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com