
分析 (1)作差便可得到x2-x-(x-2)=x2-2x+2,而配方即可得出x2-2x+2>0,从而判断出x2-x与x-2的关系;
(2)通过作差,提取公因式便可得出a3+b3-(a2b+ab2)=(a-b)2(a+b),并根据条件可以判断(a-b)2(a+b)>0,这样即可得出所比较两个式子的大小关系.
解答 解:(1)∵(x2-x)-(x-2)=x2-2x+2=(x-1)2+1≥1>0;
即(x2-x)-(x-2)>0;
∴x2-x>x-2
(2)∵(a3+b3)-(a2b+ab2)=a3+b3-a2b-ab2
=a2(a-b)-b2(a-b)
=(a-b)(a2-b2)
=(a-b)2(a+b);
∵a>0,b>0且a≠b;
∴(a-b)2>0,a+b>0;
∴(a-b)2(a+b)>0;
即(a3+b3)-(a2b+ab2)>0;
∴a3+b3>a2b+ab2.
点评 考查作差的方法比较两个代数式的大小关系,配方法的运用,以及平方差公式.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{10}$,10] | B. | ($\frac{1}{10}$,10) | C. | [$\frac{1}{10}$,1)∪(1,10] | D. | ($\frac{1}{10}$,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
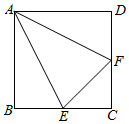 如图,正方形ABCD的边长为2,点E,F分别是BC,CD的中点,沿着AE,AF,EF把该正方形折叠成三棱锥A-PEF(点B,C,D重合于点P),则三棱锥A-PEF内切球的半径为$\frac{1}{4}$.
如图,正方形ABCD的边长为2,点E,F分别是BC,CD的中点,沿着AE,AF,EF把该正方形折叠成三棱锥A-PEF(点B,C,D重合于点P),则三棱锥A-PEF内切球的半径为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{32\sqrt{3}}{27}$π | C. | $\frac{3}{4}$π | D. | $\frac{32}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若向量$\overrightarrow a$,$\overrightarrow b$共线则向量$\overrightarrow a$,$\overrightarrow b$的方向相同 | |
| B. | 若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$则$\overrightarrow a$∥$\overrightarrow c$ | |
| C. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{CD}$是共线向量则A,B,C,D四点在一条直线上 | |
| D. | 若$\overrightarrow a$=$\overrightarrow b$,$\overrightarrow b$=$\overrightarrow c$则$\overrightarrow a$=$\overrightarrow c$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com