
| A. | 若向量$\overrightarrow a$,$\overrightarrow b$共线则向量$\overrightarrow a$,$\overrightarrow b$的方向相同 | |
| B. | 若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$则$\overrightarrow a$∥$\overrightarrow c$ | |
| C. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{CD}$是共线向量则A,B,C,D四点在一条直线上 | |
| D. | 若$\overrightarrow a$=$\overrightarrow b$,$\overrightarrow b$=$\overrightarrow c$则$\overrightarrow a$=$\overrightarrow c$ |
分析 根据平面向量的有关概念,对选项中的命题进行分析、判断即可.
解答 解:对于A,向量$\overrightarrow a$,$\overrightarrow b$共线时,向量$\overrightarrow a$,$\overrightarrow b$的方向相同或相反,故命题错误;
对于B,$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$时,$\overrightarrow a$∥$\overrightarrow c$在$\overrightarrow b$=$\overrightarrow{0}$时不一定成立,故命题错误;
对于C,向量$\overrightarrow{AB}$与向量$\overrightarrow{CD}$是共线向量,则A,B,C,D四点不一定在一条直线上,
如平行四边形ABDC中,$\overrightarrow{AB}$=$\overrightarrow{CD}$,故命题错误;
对于D,当$\overrightarrow a$=$\overrightarrow b$,$\overrightarrow b$=$\overrightarrow c$时,$\overrightarrow a$=$\overrightarrow c$,命题正确.
故选:D.
点评 本题考查了平面向量的有关概念与应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$-1)R | B. | $\frac{2-\sqrt{3}}{2}$R | C. | (2-$\sqrt{3}$)R | D. | $\frac{\sqrt{3}-1}{2}$R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
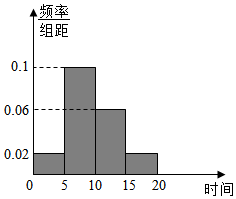 某市为了缓解交通压力,提倡低碳环保,鼓励市民乘坐公共交通系统出行.为了更好地保障市民出行,合理安排运力,有效利用公共交通资源合理调度,在某地铁站点进行试点调研市民对候车时间的等待时间(候车时间不能超过20分钟),以便合理调度减少候车时间,使市民更喜欢选择公共交通.为此在该地铁站的一些乘客中进行调查分析,得到如下统计表和各时间段人数频率分布直方图:
某市为了缓解交通压力,提倡低碳环保,鼓励市民乘坐公共交通系统出行.为了更好地保障市民出行,合理安排运力,有效利用公共交通资源合理调度,在某地铁站点进行试点调研市民对候车时间的等待时间(候车时间不能超过20分钟),以便合理调度减少候车时间,使市民更喜欢选择公共交通.为此在该地铁站的一些乘客中进行调查分析,得到如下统计表和各时间段人数频率分布直方图:| 分组 | 等待时间(分钟) | 人数 |
| 第一组 | [0,5) | 10 |
| 第二组 | [5,10) | a |
| 第三组 | [10,15) | 30 |
| 第四组 | [15,20) | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com