
| A. | ($\sqrt{3}$-1)R | B. | $\frac{2-\sqrt{3}}{2}$R | C. | (2-$\sqrt{3}$)R | D. | $\frac{\sqrt{3}-1}{2}$R |
分析 先画出过正方体对角面的截面图,设小球的半径r,通过AS=AO1+O1S建立等式,求出r即可求出要使流出来的水量最多时这个铁球的半径.
解答  解:过正方体对角面的截面图如图所示,设两球的交点为S,
解:过正方体对角面的截面图如图所示,设两球的交点为S,
AC1=2$\sqrt{3}$R,AO=$\sqrt{3}$Q,AS=AO-OS=($\sqrt{3}$-1)R,
设小球的半径r,tan∠C1AC=$\frac{\sqrt{2}}{2}$.
在△AO1D中,AO1=$\sqrt{3}$r,
∴AS=AO1+O1S,
∴($\sqrt{3}$-1)R=$\sqrt{3}$r+r.
解得:r=(2-$\sqrt{3}$)R为所求.
要使流出来的水量最多,这个铁球的半径应该为(2-$\sqrt{3}$)R.
故选:C.
点评 本题考查球与多面体相切问题,解决此类问题必须做出正确的截面(即截面一定要过球心),再运用几何知识解出所求量.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{10}$,10] | B. | ($\frac{1}{10}$,10) | C. | [$\frac{1}{10}$,1)∪(1,10] | D. | ($\frac{1}{10}$,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{32\sqrt{3}}{27}$π | C. | $\frac{3}{4}$π | D. | $\frac{32}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{2\sqrt{2}}{3}$π | C. | $\frac{4\sqrt{2}}{3}$π | D. | $\frac{8\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若向量$\overrightarrow a$,$\overrightarrow b$共线则向量$\overrightarrow a$,$\overrightarrow b$的方向相同 | |
| B. | 若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$则$\overrightarrow a$∥$\overrightarrow c$ | |
| C. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{CD}$是共线向量则A,B,C,D四点在一条直线上 | |
| D. | 若$\overrightarrow a$=$\overrightarrow b$,$\overrightarrow b$=$\overrightarrow c$则$\overrightarrow a$=$\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
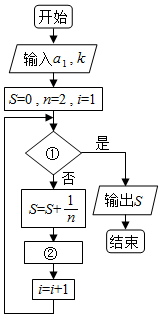 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{40}$的值的一个程序框图,则图中判断框内①处和执行框中的②处应填的语句分别是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{40}$的值的一个程序框图,则图中判断框内①处和执行框中的②处应填的语句分别是( )| A. | i>40,n=n+1 | B. | i>20,n=n+2 | C. | i>40,n=n+2 | D. | i=20,n=n+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com