
分析 设出曲线过点P切线方程的切点坐标,把切点的横坐标代入到导函数中即可表示出切线的斜率,根据切点坐标和表示出的斜率,写出切线的方程,把P的坐标代入切线方程即可得到关于切点横坐标的方程,求出方程的解即可得到切点横坐标的值,分别代入所设的切线方程即可.
解答 解:设过点P(2,$\frac{8}{3}$)的直线与曲线相切,切点坐标为$({x_0},\frac{1}{3}x_0^3)$,
所以切线的斜率为${f^'}({x_0})=x_0^2$,所以切线方程为$y-\frac{1}{3}x_0^3=x_0^2(x-{x_0})$,
因为切线过点P(2,$\frac{8}{3}$),所以$\frac{8}{3}-\frac{1}{3}x_0^3=x_0^2(2-{x_0})$,
解得x0=2或x0=-1
当x0=2时,切线方程为12x-3y-16=0
当x0=-1时,切线方程为3y-3x-2=0
所以,所求切线方程为12x-3y-16=0或3y-3x-2=0.
点评 本题考查学生会利用导数研究曲线上某点的切线方程,是一道综合题.学生在解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”;同时解决“过某点的切线”问题,一般是设出切点坐标解决.


科目:高中数学 来源: 题型:选择题
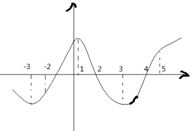
| A. | 在区间(-3,-2)内f(x)是增函数 | B. | 在(1,3)内f(x)是增函数 | ||
| C. | 当x=4时,f(x)取极大值 | D. | 当x=2时,f(x)取极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,$\frac{5π}{4}$) | B. | (0,$\frac{π}{2}$) | C. | ($\frac{π}{4}$,$\frac{3π}{2}$) | D. | (-$\frac{π}{2}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com