
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶7元,未售出的酸奶降价处理,以每瓶1.5元的价格当天全部处理完.据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 14 | 34 | 27 | 9 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),若该超市在六月份每天的进货量均为450瓶,写出
(单位:元),若该超市在六月份每天的进货量均为450瓶,写出![]() 的所有可能值,并估计
的所有可能值,并估计![]() 大于零的概率.
大于零的概率.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)当且仅当最高气温低于![]() 时这种酸奶一天的需求量不超过300瓶,由表格数据求解即可;
时这种酸奶一天的需求量不超过300瓶,由表格数据求解即可;
(2)分别讨论最高气温不低于![]() ,最高气温位于区间
,最高气温位于区间![]() (单位:
(单位:![]() ),最高气温低于
),最高气温低于![]() 的情况,进而求解;基于此,若
的情况,进而求解;基于此,若![]() 大于零,则当且仅当最高气温不低于
大于零,则当且仅当最高气温不低于![]() ,进而求解即可
,进而求解即可
(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于![]() ,
,
由表格数据知,最高气温低于![]() 的频率为
的频率为![]() ,
,
所以这种酸奶一天的需求量不超过300瓶的概率的估计值为![]()
(2)当这种酸奶一天的进货量为450瓶时,
若最高气温不低于![]() ,则
,则![]() ;
;
若最高气温位于区间![]() (单位:
(单位:![]() ),
),
则![]() ,
,
若最高气温低于![]() ,则
,则![]() ,
,
所以![]() 的所有可能值为1350,525,
的所有可能值为1350,525,![]() ,
,
若![]() 大于零,则当且仅当最高气温不低于
大于零,则当且仅当最高气温不低于![]() ,
,
由表格数据知,最高气温不低于![]() 的频率为
的频率为![]() ,
,
因此![]() 大于零的概率的估计值为
大于零的概率的估计值为![]()


科目:高中数学 来源: 题型:
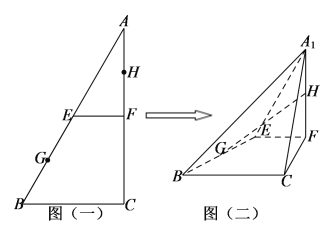
【题目】如图,三角形ABC为直角三角形,且![]() ,
,![]() ,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至
,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至![]() ,连接
,连接![]() ,
,![]() ,GH(如图二).
,GH(如图二).
(1)证明:![]() 平面
平面![]() ;
;
(2)当平面![]() 平面EFCB时,求异面直线GH与EF所成角的余弦值.
平面EFCB时,求异面直线GH与EF所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且抛物线
,且抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的一个焦点.
的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() (
(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名,其评估成绩![]() 近似的服从正态分布
近似的服从正态分布![]() .现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
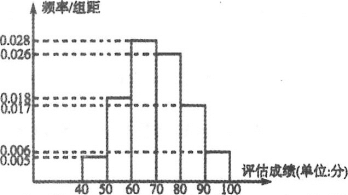
(1)求样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若学校规定评估成绩超过![]() 分的毕业生可参加
分的毕业生可参加![]() 三家公司的面试.
三家公司的面试.
(ⅰ)用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
(ⅱ)若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为![]() ,李华准备依次从
,李华准备依次从![]() 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择
三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择![]() 公司的哪些岗位?
公司的哪些岗位?
并说明理由.
附:![]() ,若随机变量
,若随机变量![]() ,
,
则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 分别为其左、右焦点,
分别为其左、右焦点,![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作关于轴
作关于轴![]() 对称的两条不同的直线
对称的两条不同的直线![]() ,若直线
,若直线![]() 交椭圆
交椭圆![]() 于一点
于一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于一点
于一点![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和椭圆
和椭圆![]() . 直线
. 直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(Ⅰ) 求椭圆![]() 的离心率;
的离心率;
(Ⅱ) 当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值 .
的值 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中:①双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;②设
有相同的焦点;②设![]() 、
、![]() 是两个定点,
是两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线的一支;③设点
的轨迹为双曲线的一支;③设点![]() 、
、![]() 分别是定圆
分别是定圆![]() 上一个定点和动点,
上一个定点和动点,![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com