
【题目】如图,三角形ABC为直角三角形,且![]() ,
,![]() ,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至
,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至![]() ,连接
,连接![]() ,
,![]() ,GH(如图二).
,GH(如图二).
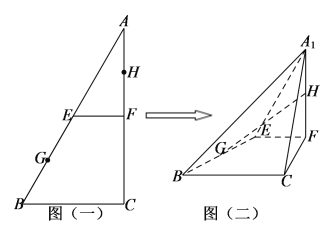
(1)证明:![]() 平面
平面![]() ;
;
(2)当平面![]() 平面EFCB时,求异面直线GH与EF所成角的余弦值.
平面EFCB时,求异面直线GH与EF所成角的余弦值.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线方程![]() ,
,![]() 为焦点,
为焦点,![]() 为抛物线准线上一点,
为抛物线准线上一点,![]() 为线段
为线段![]() 与抛物线的交点,定义:
与抛物线的交点,定义:![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)证明:存在常数![]() ,使得
,使得![]() .
.
(3)![]() 为抛物线准线上三点,且
为抛物线准线上三点,且![]() ,判断
,判断![]() 与
与![]() 的关系.
的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
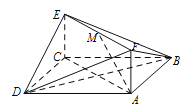
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)证明:存在点![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列A:
,数列A:![]() ,
,![]() ,…
,…![]() 中的项均为不大于
中的项均为不大于![]() 的正整数.
的正整数.![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的个数(
的个数(![]() ).定义变换
).定义变换![]() ,
,![]() 将数列
将数列![]() 变成数列
变成数列![]() :
:![]() ,
,![]() ,…
,…![]() 其中
其中![]() .
.
(1)若![]() ,对数列
,对数列![]() :
:![]() ,写出
,写出![]() 的值;
的值;
(2)已知对任意的![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() .求证:
.求证:![]() (
(![]() )的充分必要条件为
)的充分必要条件为![]() (
(![]() );
);
(3)若![]() ,对于数列
,对于数列![]() :
:![]() ,
,![]() ,…
,…![]() ,令
,令![]() :
:![]() ,求证:
,求证:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ:![]() +
+![]() =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为![]() .
.
(1)求椭圆Γ的标准方程;
(2)过P(1,0)作动直线AB交椭圆Γ于A,B两点,Q(4,3)为平面上一定点连接QA,QB,设直线QA,QB的斜率分别为k1,k2,问k1+k2是否为定值,如果是,则求出该定值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() 的零点构成一个公差为
的零点构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图像沿
的图像沿![]() 轴向左平移
轴向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像,关于函数
的图像,关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 在![]() 上是增函数
上是增函数
B. 其图像关于![]() 对称
对称
C. 函数![]() 是奇函数
是奇函数
D. 在区间![]() 上的值域为[-2,1]
上的值域为[-2,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
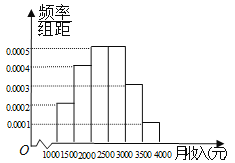
(1)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,求月收入在![]() (元)段应抽出的人数;
(元)段应抽出的人数;
(2)为了估计该社区3个居民中恰有2个月收入在![]() (元)的概率,采用随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,我们用0,1,2,3,4表示收入在
(元)的概率,采用随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,我们用0,1,2,3,4表示收入在![]() (元)的居民,剩余的数字表示月收入不在
(元)的居民,剩余的数字表示月收入不在![]() (元)的居民;再以每三个随机数为一组,代表统计的结果,经随机模拟产生了20组随机数如下:
(元)的居民;再以每三个随机数为一组,代表统计的结果,经随机模拟产生了20组随机数如下:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,计算该社区3个居民中恰好有2个月收入在![]() (元)的概率.
(元)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,点
,点![]() ,点
,点![]() 是平面直角坐标系内的动点,且点
是平面直角坐标系内的动点,且点![]() 到直线
到直线![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍.记动点
的距离的2倍.记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() (
(![]() 是坐标系原点)的面积为
是坐标系原点)的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若(2)中过点![]() 的直线
的直线![]() 是倾斜角不为0的任意直线,仍记
是倾斜角不为0的任意直线,仍记![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,设点
,设点![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶7元,未售出的酸奶降价处理,以每瓶1.5元的价格当天全部处理完.据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 14 | 34 | 27 | 9 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),若该超市在六月份每天的进货量均为450瓶,写出
(单位:元),若该超市在六月份每天的进货量均为450瓶,写出![]() 的所有可能值,并估计
的所有可能值,并估计![]() 大于零的概率.
大于零的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com