
【题目】已知![]() ,数列A:
,数列A:![]() ,
,![]() ,…
,…![]() 中的项均为不大于
中的项均为不大于![]() 的正整数.
的正整数.![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的个数(
的个数(![]() ).定义变换
).定义变换![]() ,
,![]() 将数列
将数列![]() 变成数列
变成数列![]() :
:![]() ,
,![]() ,…
,…![]() 其中
其中![]() .
.
(1)若![]() ,对数列
,对数列![]() :
:![]() ,写出
,写出![]() 的值;
的值;
(2)已知对任意的![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() .求证:
.求证:![]() (
(![]() )的充分必要条件为
)的充分必要条件为![]() (
(![]() );
);
(3)若![]() ,对于数列
,对于数列![]() :
:![]() ,
,![]() ,…
,…![]() ,令
,令![]() :
:![]() ,求证:
,求证:![]() (
(![]() ).
).
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据定义,![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的个数,即可由数列
的个数,即可由数列![]() 得
得![]() 的值.
的值.
(2)根据对任意的![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() ,由充分必要条件的判定,分必要性与充分性两步分别证明即可.
,由充分必要条件的判定,分必要性与充分性两步分别证明即可.
(3)设![]() :
:![]() ,
,![]() ,…
,…![]() 的所有不同取值为
的所有不同取值为![]() ,且满足:
,且满足:![]() .设
.设![]() .根据
.根据![]() ,结合题意中的
,结合题意中的![]() 变换可得
变换可得![]() :
:![]() ,
,![]() ,
,![]() ,即可证明
,即可证明![]() (
(![]() ).
).
(1)∵![]() ,对数列
,对数列![]() :
:![]() ,
,
∴![]() .
.
(2)证明:由于对任意的正整数![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() .所以
.所以![]() 均不为零.
均不为零.
必要性:![]() (
(![]() ),由于
),由于![]() ,
,
∴![]() ;
;![]() ;
;![]() ;…;
;…;![]() .
.
通过解此方程组,可得![]() (
(![]() )成立.
)成立.
充分性:若![]() (
(![]() )成立,不妨设
)成立,不妨设![]() (
(![]() ),可以得到
),可以得到![]()
∴![]() ;
;![]() ;
;![]() ;…;
;…;![]() .
.
∴![]() (
(![]() )成立.
)成立.
故![]() (
(![]() )的充分必要条件为
)的充分必要条件为![]() (
(![]() )
)
(3)证明:设![]() :
:![]() ,
,![]() ,…
,…![]() 的所有不同取值为
的所有不同取值为![]() ,且满足:
,且满足:![]() .
.
不妨设![]() ,
,
其中![]() ;
;![]() ;…;
;…;![]() .
.
又∵![]() ,根据变换
,根据变换![]() 有:
有:![]() ;
;![]() ;…;
;…;![]() ;
;
∴![]() :
:![]() ,
,![]() ,
,![]() ,
,
即![]() :
:![]() ,
,![]() ,
,![]() ,
,
∴![]() :
:![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,…,
,…,![]() .
.
∴![]() ,
,![]()
即![]() :
:![]() ,
,![]() ,
,![]() ,
,
从而![]() (
(![]() ).
).
故![]() (
(![]() )
)


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:
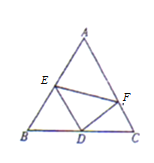
【题目】某公司航拍宣传画报,为了凸显公司文化,选择如图所示的边长为2百米的正三角形![]() 空地进行布置拍摄场景,在
空地进行布置拍摄场景,在![]() 的中点
的中点![]() 处安装中央聚光灯,
处安装中央聚光灯,![]() 为边
为边![]() 上得可以自由滑动的动点,其中
上得可以自由滑动的动点,其中![]() 设置为普通色彩灯带(灯带长度可以自由伸缩),线段
设置为普通色彩灯带(灯带长度可以自由伸缩),线段![]() 部分需要材料
部分需要材料![]() (单位:百米)装饰用以增加拍摄效果因材料
(单位:百米)装饰用以增加拍摄效果因材料![]() 价格昂贵,所以公司要求采购
价格昂贵,所以公司要求采购![]() 材料使用不造成浪费.
材料使用不造成浪费.
(1)当![]() ,
,![]() 与
与![]() 垂直时,采购部需要采购多少百米材料
垂直时,采购部需要采购多少百米材料![]() ?
?
(2)为了增加拍摄动态效果需要,现要求点![]() 在
在![]() 边上滑动,且
边上滑动,且![]() ,则购买材料
,则购买材料![]() 的范围是多少才能满足动态效果需要又不会造成浪费.
的范围是多少才能满足动态效果需要又不会造成浪费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员进行某商品的市场营销调查时发现,每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到以下表:
反馈点数t | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(Ⅰ)经分析发现,可用线性回归模型![]() 拟合当地该商品销量
拟合当地该商品销量![]() (千件)与返还点数
(千件)与返还点数![]() 之间的相关关系.试预测若返回6个点时该商品每天的销量;
之间的相关关系.试预测若返回6个点时该商品每天的销量;
(Ⅱ)若节日期间营销部对商品进行新一轮调整.已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间 (百分比) | [1,3) | [3,5) | [5,7) | [7,9) | [9,11) | [11,13) |
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,求抽出的3人中至少有1名“欲望膨胀型”消费者的概率.
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,求抽出的3人中至少有1名“欲望膨胀型”消费者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
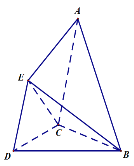
【题目】已知空间几何体![]() 中,
中,![]() 与
与![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形,![]() 为腰长为
为腰长为![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)试在平面![]() 内作一条直线,使直线上任意一点
内作一条直线,使直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明
平行,并给出详细证明
(2)求点![]() 到平面
到平面![]() 的距离
的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且![]() .
.
(1)求抛物线C的方程;
(2)动直线l:x=my+1(m![]() R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
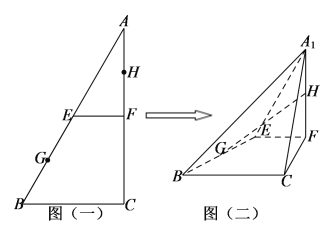
【题目】如图,三角形ABC为直角三角形,且![]() ,
,![]() ,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至
,E,F分别为AB,AC的中点,G,H分别为BE,AF的中点(如图一),现在沿EF将三角形AEF折起至![]() ,连接
,连接![]() ,
,![]() ,GH(如图二).
,GH(如图二).
(1)证明:![]() 平面
平面![]() ;
;
(2)当平面![]() 平面EFCB时,求异面直线GH与EF所成角的余弦值.
平面EFCB时,求异面直线GH与EF所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com