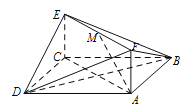
【题目】已知空间几何体
中，
与
均为边长为
的等边三角形，
为腰长为
的等腰三角形，平面
平面
，平面
平面.
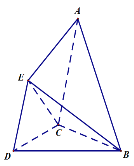
（1）试在平面内作一条直线，使直线上任意一点
与
的连线
均与平面
平行，并给出详细证明
（2）求点
到平面
的距离
【答案】（1）见解析；（2）
【解析】
（1）取BC和BD的中点H、G，利用面面平行的判断定理证得平面CDE平行平面AHG即可求得结果；
（2）分别求得三角形ABC和CDE的面积以及求得E到平面ABC的距离，再利用等体积法
即可求得
到平面
的距离.
如图所示:取BC和BD的中点H、G，连接HG，HG为所求直线，
证明如下：因为BC和BD的中点H、G，所以
,
又平面
平面
，且
平面BCD
又平面
平面.
,得
，
所以
，即
所以
，所以直线HG上任意一点
与
的连线
均与平面
平行.
由（1）可得，即
平面ABC
所以点E到平面ABC的距离和点O到平面ABC的距离相等，记为
三角形ABC的面积
而三角形ACE的面积
用等体积法可得：
科目：高中数学 来源： 题型：
【题目】如图，
，
，
，
，
分别为
，
边的中点，以
为折痕把
折起，使点
到达点
的位置，且
..
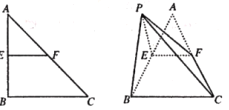
（Ⅰ）证明：
平面
；
（Ⅱ）设
为线段
上动点，求直线
与平面
所成角的正弦值的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】奖饭店推出甲.乙两种新菜品，为了了解两种菜品的受欢迎程度，现统计一周内两种菜品每天的销售量，得到下面的茎叶图.下列说法中，不正确的是（ ）
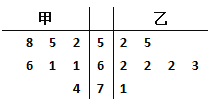
A.甲菜品销售量的众数比乙菜品销售量的众数小
B.甲菜品销售量的中位数比乙菜品销售量的中位数小
C.甲菜品销售量的平均值比乙菜品销售量的平均值大
D.甲菜品销售量的方差比乙菜品销售量的方差大.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正方形
和矩形
所在的平面互相垂直，
，点
在线段
上.
（Ⅰ）若为的中点，求证：
平面
；
（Ⅱ）求二面角
的余弦值；
（Ⅲ）证明：存在点，使得
平面
，并求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（l）根据表中数据，请建立关于的回归直线方程：
（2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：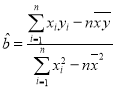
，
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，数列A：
，
，…
中的项均为不大于
的正整数.
表示，，…中
的个数（
）.定义变换
，将数列
变成数列
：
，
，…
其中
.
（1）若
，对数列：
，写出
的值；
（2）已知对任意的（
），存在中的项
，使得
.求证：
（
）的充分必要条件为
（
）；
（3）若
，对于数列：，，…，令
：
，求证：
（）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知函数
的零点构成一个公差为
的等差数列，把函数
的图像沿
轴向左平移
个单位，得到函数
的图像，关于函数,下列说法正确的是（ ）
A. 在
上是增函数
B. 其图像关于
对称
C. 函数是奇函数
D. 在区间
上的值域为[-2，1]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱锥
，底面
为菱形，
,
为
上的点，过
的平面分别交
，
于点
，
，且
平面
．
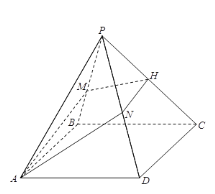
（1）证明：
；
（2）当为的中点，
，
与平面所成的角为
，求
与平面所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
