
【题目】己知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间和极值;
的单调区间和极值;
(2)讨论![]() 的零点的个数.
的零点的个数.
【答案】(1)见解析;(2)当![]() 或
或![]() 时,
时,![]() 有1个零点;当
有1个零点;当![]() 且
且![]() 时,
时,![]() 有2个零点.
有2个零点.
【解析】
(1)利用导数证明函数的单调性以及即可;
(2)对参数![]() 的值进行分类讨论,确定函数
的值进行分类讨论,确定函数![]() 的单调性,结合零点存在性定理判断零点的个数.
的单调性,结合零点存在性定理判断零点的个数.
(1)![]() 的定义域为
的定义域为![]() ,
,![]()
![]()
![]()
则![]() 在
在![]() 上单调递增
上单调递增
又![]() ,所以当
,所以当![]() 时,
时,![]()
当![]() 时,
时,![]()
即![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
故![]() 的极小值为
的极小值为![]() ,
,![]() 无极大值
无极大值
(2)当![]() 时,由(1)知
时,由(1)知![]()
故![]() 仅有一个零点
仅有一个零点![]() ;
;
当![]() 时,
时,![]() ,令
,令![]()
![]() ;
;
令![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
令![]() ,所以
,所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,![]() ,
,
所以![]() ,最小值
,最小值![]() 与0的比较等价于
与0的比较等价于![]() 与0的大小比较,
与0的大小比较,
所以分三类进行讨论:
①当![]() 时,即
时,即![]() 时,由
时,由![]() 在
在![]() 上单调递减及在
上单调递减及在![]() 上单调递增,且
上单调递增,且![]() ,
,![]()
由零点存在定理,得![]() 在
在![]() 上存在唯一零点,设为
上存在唯一零点,设为![]() 所以
所以
|
|
|
| 0 |
|
|
| 0 |
| 0 |
|
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
又![]() 及
及![]()
![]()
由零点存在定理,得![]() 在
在![]() 上存在唯一零点,设为
上存在唯一零点,设为![]() ,
,
综上,当![]() 时,
时,![]() 在
在![]() 上存在2个零点(一个为
上存在2个零点(一个为![]() ,一个为
,一个为![]() );
);
②当![]() 时,即
时,即![]() 时,由
时,由![]() 在
在![]() 上单调递减及在
上单调递减及在![]() 上单调递增,
上单调递增,
且![]() ,得
,得![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 上只有一个零点
上只有一个零点![]() ;
;
③当![]() 时,同理可得
时,同理可得![]() 在
在![]() 上存在2个零点:一个为
上存在2个零点:一个为![]() ,一个为
,一个为![]()
综上可得,当![]() 或
或![]() 时,
时,![]() 有1个零点;
有1个零点;
当![]() 且
且![]() 时,
时,![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】奖饭店推出甲.乙两种新菜品,为了了解两种菜品的受欢迎程度,现统计一周内两种菜品每天的销售量,得到下面的茎叶图.下列说法中,不正确的是( )
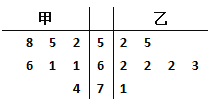
A.甲菜品销售量的众数比乙菜品销售量的众数小
B.甲菜品销售量的中位数比乙菜品销售量的中位数小
C.甲菜品销售量的平均值比乙菜品销售量的平均值大
D.甲菜品销售量的方差比乙菜品销售量的方差大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列A:
,数列A:![]() ,
,![]() ,…
,…![]() 中的项均为不大于
中的项均为不大于![]() 的正整数.
的正整数.![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的个数(
的个数(![]() ).定义变换
).定义变换![]() ,
,![]() 将数列
将数列![]() 变成数列
变成数列![]() :
:![]() ,
,![]() ,…
,…![]() 其中
其中![]() .
.
(1)若![]() ,对数列
,对数列![]() :
:![]() ,写出
,写出![]() 的值;
的值;
(2)已知对任意的![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() .求证:
.求证:![]() (
(![]() )的充分必要条件为
)的充分必要条件为![]() (
(![]() );
);
(3)若![]() ,对于数列
,对于数列![]() :
:![]() ,
,![]() ,…
,…![]() ,令
,令![]() :
:![]() ,求证:
,求证:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() 的零点构成一个公差为
的零点构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图像沿
的图像沿![]() 轴向左平移
轴向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像,关于函数
的图像,关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 在![]() 上是增函数
上是增函数
B. 其图像关于![]() 对称
对称
C. 函数![]() 是奇函数
是奇函数
D. 在区间![]() 上的值域为[-2,1]
上的值域为[-2,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
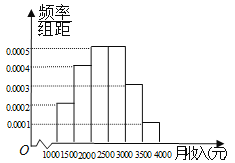
(1)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,求月收入在![]() (元)段应抽出的人数;
(元)段应抽出的人数;
(2)为了估计该社区3个居民中恰有2个月收入在![]() (元)的概率,采用随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,我们用0,1,2,3,4表示收入在
(元)的概率,采用随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,我们用0,1,2,3,4表示收入在![]() (元)的居民,剩余的数字表示月收入不在
(元)的居民,剩余的数字表示月收入不在![]() (元)的居民;再以每三个随机数为一组,代表统计的结果,经随机模拟产生了20组随机数如下:
(元)的居民;再以每三个随机数为一组,代表统计的结果,经随机模拟产生了20组随机数如下:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,计算该社区3个居民中恰好有2个月收入在![]() (元)的概率.
(元)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为积极响应国家“阳光体育运动”的号召,某学校在了解到学生的实际运动情况后,发起以“走出教室,走到操场,走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况,从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样,收集300位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图。

(1)据图估计该校学生每周平均体育运动时间.并估计高一年级每周平均体育运动时间不足4小时的人数;
(2)规定每周平均体育运动时间不少于6小时记为“优秀”,否则为“非优秀”,在样本数据中,有30位高三学生的每周平均体育运动时间不少于6小时,请完成下列![]() 列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,点
,点![]() ,点
,点![]() 是平面直角坐标系内的动点,且点
是平面直角坐标系内的动点,且点![]() 到直线
到直线![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍.记动点
的距离的2倍.记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() (
(![]() 是坐标系原点)的面积为
是坐标系原点)的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若(2)中过点![]() 的直线
的直线![]() 是倾斜角不为0的任意直线,仍记
是倾斜角不为0的任意直线,仍记![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,设点
,设点![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
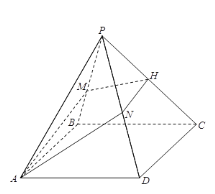
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com