
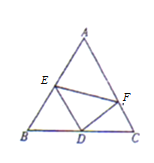
【题目】某公司航拍宣传画报,为了凸显公司文化,选择如图所示的边长为2百米的正三角形![]() 空地进行布置拍摄场景,在
空地进行布置拍摄场景,在![]() 的中点
的中点![]() 处安装中央聚光灯,
处安装中央聚光灯,![]() 为边
为边![]() 上得可以自由滑动的动点,其中
上得可以自由滑动的动点,其中![]() 设置为普通色彩灯带(灯带长度可以自由伸缩),线段
设置为普通色彩灯带(灯带长度可以自由伸缩),线段![]() 部分需要材料
部分需要材料![]() (单位:百米)装饰用以增加拍摄效果因材料
(单位:百米)装饰用以增加拍摄效果因材料![]() 价格昂贵,所以公司要求采购
价格昂贵,所以公司要求采购![]() 材料使用不造成浪费.
材料使用不造成浪费.
(1)当![]() ,
,![]() 与
与![]() 垂直时,采购部需要采购多少百米材料
垂直时,采购部需要采购多少百米材料![]() ?
?
(2)为了增加拍摄动态效果需要,现要求点![]() 在
在![]() 边上滑动,且
边上滑动,且![]() ,则购买材料
,则购买材料![]() 的范围是多少才能满足动态效果需要又不会造成浪费.
的范围是多少才能满足动态效果需要又不会造成浪费.
【答案】(1)![]() (百米);
(百米);
(2)![]() (单位为百米).
(单位为百米).
【解析】
(1)因为![]() 与
与![]() 垂直,所以三角形
垂直,所以三角形![]() 是直角三角形,利用锐角三角函数,可以求出
是直角三角形,利用锐角三角函数,可以求出![]() 的长,这样可以求出
的长,这样可以求出![]() 的长,在
的长,在![]() 中,利用正弦定理可以求出
中,利用正弦定理可以求出![]() 的长,这样可以求出
的长,这样可以求出![]() 的长,这样可以求出采购部需要采购材料
的长,这样可以求出采购部需要采购材料![]() 的数量;
的数量;
(2)设![]() ,根据
,根据![]() ,可以求出
,可以求出![]() 的取值范围,由
的取值范围,由![]() 和三角形
和三角形![]() 等边三角形,可以证明出
等边三角形,可以证明出![]() 与
与![]() 相似,这样可以得到
相似,这样可以得到![]() 之间的关系,这样
之间的关系,这样![]() 可以用关于
可以用关于![]() 的式子表示,构造函数,利用函数的单调性,求出
的式子表示,构造函数,利用函数的单调性,求出![]() 的取值范围.
的取值范围.
(1)三角形![]() 等边三角形,
等边三角形,![]() 是
是![]() 的中点,因此
的中点,因此![]() ,
,![]() ,因为
,因为![]() 与
与![]() 重直,所以三角形
重直,所以三角形![]() 是直角三角形,因此有
是直角三角形,因此有![]() ,
,
所以![]() ,因此
,因此![]() ,在
,在![]() 中,由正弦定理可知:
中,由正弦定理可知:
![]() ,
, 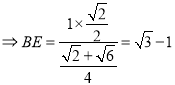 ,因此
,因此![]() ,所以采购部需要采购材料
,所以采购部需要采购材料![]() 为
为![]() (百米);
(百米);
(2)设![]() ,当
,当![]() 与
与![]() 重合时,由
重合时,由![]() ,可求得
,可求得![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,而
,而![]() ,
,
所以![]() ,
,![]() ,因此
,因此![]() 与
与![]() 相似,
相似,
所以有![]() ,设
,设![]() ,
,![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,故当
单调递减,故当![]() 时,
时,![]() 有最大值2,
有最大值2,
![]() ,所以
,所以![]() ,购买材料
,购买材料![]() 的范围是
的范围是![]() (单位为百米).
(单位为百米).


科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
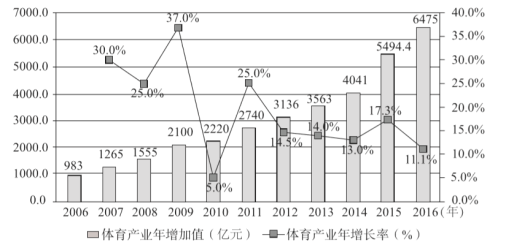
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[ 0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:

假设甲、乙两种酸奶独立销售且日销售量相互独立.
(1)写出频率分布直方图(甲)中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设![]() 表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求
表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点,以
边的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ..
..
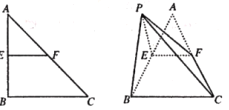
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 为线段
为线段![]() 上动点,求直线
上动点,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 、
、![]() 的交点记为
的交点记为![]() .
.
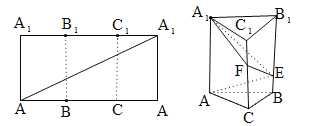
(1)在三棱柱![]() 中,若过
中,若过![]() 三点做一平面,求截得的几何体
三点做一平面,求截得的几何体![]() 的表面积;
的表面积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() 和
和![]() ,记过点
,记过点![]() ,
,![]() 的直线的斜率为k,问:是否存在m,使得
的直线的斜率为k,问:是否存在m,使得![]() ?若存在,求出m的值;若不存在,请说明理由.
?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程![]() ,
,![]() 为焦点,
为焦点,![]() 为抛物线准线上一点,
为抛物线准线上一点,![]() 为线段
为线段![]() 与抛物线的交点,定义:
与抛物线的交点,定义:![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)证明:存在常数![]() ,使得
,使得![]() .
.
(3)![]() 为抛物线准线上三点,且
为抛物线准线上三点,且![]() ,判断
,判断![]() 与
与![]() 的关系.
的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奖饭店推出甲.乙两种新菜品,为了了解两种菜品的受欢迎程度,现统计一周内两种菜品每天的销售量,得到下面的茎叶图.下列说法中,不正确的是( )
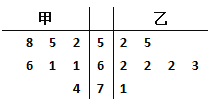
A.甲菜品销售量的众数比乙菜品销售量的众数小
B.甲菜品销售量的中位数比乙菜品销售量的中位数小
C.甲菜品销售量的平均值比乙菜品销售量的平均值大
D.甲菜品销售量的方差比乙菜品销售量的方差大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列A:
,数列A:![]() ,
,![]() ,…
,…![]() 中的项均为不大于
中的项均为不大于![]() 的正整数.
的正整数.![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的个数(
的个数(![]() ).定义变换
).定义变换![]() ,
,![]() 将数列
将数列![]() 变成数列
变成数列![]() :
:![]() ,
,![]() ,…
,…![]() 其中
其中![]() .
.
(1)若![]() ,对数列
,对数列![]() :
:![]() ,写出
,写出![]() 的值;
的值;
(2)已知对任意的![]() (
(![]() ),存在
),存在![]() 中的项
中的项![]() ,使得
,使得![]() .求证:
.求证:![]() (
(![]() )的充分必要条件为
)的充分必要条件为![]() (
(![]() );
);
(3)若![]() ,对于数列
,对于数列![]() :
:![]() ,
,![]() ,…
,…![]() ,令
,令![]() :
:![]() ,求证:
,求证:![]() (
(![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com