
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
分析 根据题意,分析可得函数f(x)为偶函数,进而可得a=f(-3)=f(3),由对数函数的性质可得f(x)在区间(0,+∞)上为增函数,分析可得f($\frac{1}{4}$)<f(2)<f(3),即可得答案.
解答 解:根据题意,函数y=f(x)的图象关于y轴对称,则函数f(x)为偶函数,
则有a=f(-3)=f(3),
当x∈(0,+∞)时,f(x)=log2x,则f(x)在区间(0,+∞)上为增函数,
又由$\frac{1}{4}$<2<3,则有f($\frac{1}{4}$)<f(2)<f(3),
即a>c>b,
故选:D.
点评 本题考查函数的奇偶性与单调性的综合应用,涉及对数函数的单调性,注意利用函数的奇偶性分析f(-3)=f(3)的关系.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线C是直线且过点(-1,2) | B. | 曲线C是直线且斜率为$\frac{{\sqrt{3}}}{3}$ | ||
| C. | 曲线C是圆且圆心为(-1,2) | D. | 曲线C是圆且半径为|t| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )
某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( )| A. | 甲城销售额多,乙城不够稳定 | B. | 甲城销售额多,乙城稳定 | ||
| C. | 乙城销售额多,甲城稳定 | D. | 乙城销售额多,甲城不够稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 21 | D. | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组| A. | 32 | B. | 40 | C. | 48 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
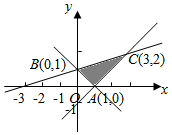 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com