
【题目】如图所示,![]() ,
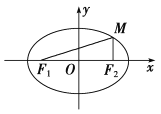
,![]() 分别为椭圆的左,右焦点,椭圆上点
分别为椭圆的左,右焦点,椭圆上点![]() 的横坐标等于右焦点的横坐标,其纵坐标等于短半轴长的
的横坐标等于右焦点的横坐标,其纵坐标等于短半轴长的![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设椭圆的长半轴、短半轴、半焦距长分别为a、b、c,可得M(c,![]() b),利用勾股定理与椭圆的定义建立关于a、b、c的等式,化简整理得b
b),利用勾股定理与椭圆的定义建立关于a、b、c的等式,化简整理得b![]() a,从而得出c
a,从而得出c![]() a,即可算出该椭圆的离心率.
a,即可算出该椭圆的离心率.
设椭圆的长半轴、短半轴、半焦距长分别为a、b、c,
可得焦点为F1(﹣c,0)、F2(c,0),点M的坐标为(c,![]() b),
b),
∵Rt△MF1F2中,F1F2⊥MF2,
∴|F1F2|2+|MF2|2=|MF1|2,即4c2![]() b2=|MF1|2,
b2=|MF1|2,
根据椭圆的定义得|MF1|+|MF2|=2a,
可得|MF1|2=(2a﹣|MF2|)2=(2a![]() b)2,
b)2,
∴(2a![]() b)2=4c2
b)2=4c2![]() b2,整理得4c2=4a2
b2,整理得4c2=4a2![]() ab,
ab,
可得3(a2﹣c2)=2ab,所以3b2=2ab,解得b![]() a,
a,
∴c![]() a,因此可得e
a,因此可得e![]() ,
,
即该椭圆的离心率等于![]() .
.
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() 且经过点P(2
且经过点P(2![]() ,
,![]() ).
).
(1)求椭圆C的方程;
(2)若椭圆C的左右顶点分别为A,B,过点A斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.是否存在定点Q,对于任意的k(k≠0)都有BD⊥EQ,若存在,求△AQD的面积的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点![]() 分别与两个定点
分别与两个定点![]() ,
,![]() 的连线的斜率之积为
的连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() ,
,![]() 两点,判断直线
两点,判断直线![]() 与以线段
与以线段![]() 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
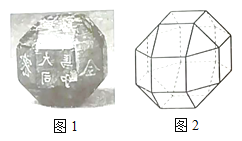
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在区间D上是增函数,且函数y=![]() 在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
①函数f(x)=-x+![]() 是区间(0,1)上的“H函数”;
是区间(0,1)上的“H函数”;
②函数g(x)=![]() 是区间(0,1)上的“H函数”.下列判断正确的是( )
是区间(0,1)上的“H函数”.下列判断正确的是( )
A. ![]() 和
和![]() 均为真命题 B.
均为真命题 B. ![]() 为真命题,
为真命题,![]() 为假命题
为假命题
C. ![]() 为假命题,
为假命题,![]() 为真命题 D.
为真命题 D. ![]() 和
和![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com