
分析 (1)由条件利用排列数、组合数的计算公式,求得n的值.
(2)在所给的二项式中,令x=0求得a0=1,再令x=1,可得 a0+a1+a2+a3+…+an的值,从而求得x=1,可得a1+a2+a3+…+an的值.
解答 解:(1)由An4=24Cn6,可得$\frac{n!}{(n-4)!}$=24•$\frac{n!}{(n-6)!•6!}$,(n-4)(n-5)=5×6,
求得n=10或n=-1(舍去),故n=10.
(2)在(1-2x)n=a0+a1x+a2x2+a3x3+…+anxn中,
令x=0,可得a0=1;
再令x=1,可得 a0+a1+a2+a3+…+an=a0+a1+a2+a3+…+a10=1,
∴a1+a2+a3+…+an的=a1+a2+a3+…+a10=0.
点评 本题主要考查排列数、组合数的计算公式,二项式定理的应用,属于给变量赋值问题,属于基础题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
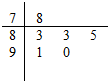 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶如图所示,给出关于该同学数学成绩的以下说法:| A. | ①② | B. | ③④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com