
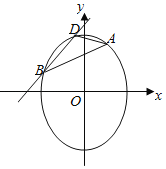
【题目】已知点A(1,![]() )是离心率为
)是离心率为![]() 的椭圆C:
的椭圆C:![]() (a>b>0)上的一点,斜率为
(a>b>0)上的一点,斜率为![]() 的直线BD交椭圆C于B、D两点,且A、B、D三点不重合
的直线BD交椭圆C于B、D两点,且A、B、D三点不重合
(1)求椭圆C的方程;
(2)求证:直线AB,AD的斜率之和为定值
(3)△ABD面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
【答案】(1)![]() .(2)见解析(3)存在,最大值为
.(2)见解析(3)存在,最大值为![]() .
.
【解析】
(1)由已知解方程组 即可;
即可;
(2)设出直线BD的方程,联立椭圆方程,利用韦达定理解决;
(3)将△ABD面积表示成![]() ,再利用基本不等式求得最值.
,再利用基本不等式求得最值.
(1)∵点A(1,![]() )是离心率为
)是离心率为![]() 的椭圆C:
的椭圆C:![]() (a>b>0)上的一点,
(a>b>0)上的一点,
∴ ,解得a=2,
,解得a=2,![]() ,
,![]() ,
,
∴椭圆C的方程为![]() .
.
(2)证明:设D(x1,y1),B(x2,y2),
设直线BD的方程为![]() ,
,
直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB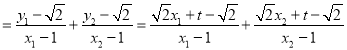
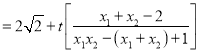 ,(*)
,(*)
联立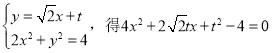 ,
,
∴△=﹣8t2+64>0,解得﹣2![]() t<2
t<2![]() ,
,![]() ,﹣﹣﹣﹣①,
,﹣﹣﹣﹣①,![]() ②,
②,
将①、②式代入*式整理得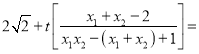 0,
0,
∴kAD+kAB=0,∴直线AB,AD的斜率之和为定值.
(3)|BD|![]() |x1﹣x2|
|x1﹣x2|![]() ,
,
设d为点A到直线BD:![]() 的距离,∴
的距离,∴![]() ,
,
∴![]() ,
,
当且仅当t=±2时取等号,
∵±2![]() ,∴当t=±2时,△ABD的面积最大,最大值为
,∴当t=±2时,△ABD的面积最大,最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现中华民族伟大复兴之梦,把我国建设成为富强民主文明和谐美丽的社会主义现代化强国,党和国家为劳动者开拓了宽广的创造性劳动的舞台.借此“东风”,某大型现代化农场在种植某种大棚有机无公害的蔬菜时,为创造更大价值,提高亩产量,积极开展技术创新活动.该农场采用了延长光照时间和降低夜间温度两种不同方案.为比较两种方案下产量的区别,该农场选取了40间大棚(每间一亩),分成两组,每组20间进行试点.第一组采用延长光照时间的方案,第二组采用降低夜间温度的方案.同时种植该蔬菜一季,得到各间大棚产量数据信息如下图:
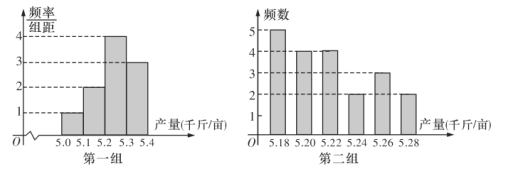
(1)如果你是该农场的负责人,在只考虑亩产量的情况下,请根据图中的数据信息,对于下一季大棚蔬菜的种植,说出你的决策方案并说明理由;
(2)已知种植该蔬菜每年固定的成本为6千元/亩.若采用延长光照时间的方案,光照设备每年的成本为0.22千元/亩;若采用夜间降温的方案,降温设备的每年成本为0.2千元/亩.已知该农场共有大棚100间(每间1亩),农场种植的该蔬菜每年产出两次,且该蔬菜市场的收购均价为1千元/千斤.根据题中所给数据,用样本估计总体,请计算在两种不同的方案下,种植该蔬菜一年的平均利润;
(3)农场根据以往该蔬菜的种植经验,认为一间大棚亩产量超过5.25千斤为增产明显.在进行夜间降温试点的20间大棚中随机抽取3间,记增产明显的大棚间数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2y,过点(0,2)作直线l交抛物线于A、B两点.
(1)证明:OA⊥OB;
(2)若直线l的斜率为1,过点A、B分别作抛物线的切线l1,l2,若直线l1,l2,相交于点P,直线l1,l2交x轴分别于点M,N,求△MNP的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地在每周六的晚上8点到10点半举行灯光展,灯光展涉及到10000盏灯,每盏灯在某一时刻亮灯的概率均为![]() ,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:
,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:![]() ),得到下面的频数表:
),得到下面的频数表:
亮灯时长/ |
|
|
|
|
|
频数 | 10 | 20 | 40 | 20 | 10 |
以样本中100盏灯的平均亮灯时长作为一盏灯的亮灯时长.
(1)试估计![]() 的值;
的值;
(2)设![]() 表示这10000盏灯在某一时刻亮灯的数目.
表示这10000盏灯在某一时刻亮灯的数目.
①求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() ;
;
②若随机变量![]() 满足
满足![]() ,则认为
,则认为![]() .假设当
.假设当![]() 时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
附:
①某盏灯在某一时刻亮灯的概率![]() 等于亮灯时长与灯光展总时长的商;
等于亮灯时长与灯光展总时长的商;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com