
分析 运用配方,可知函数表示x轴上一点P(x,0)到定点A(2,1),B(-1,-2)的距离,由于A,B分别在x轴的两边,连接AB,由两点之间线段最短,计算即可得到最小值.
解答 解:函数y=$\sqrt{{x}^{2}-4x+5}$+$\sqrt{{x}^{2}+2x+5}$
=$\sqrt{(x-2)^{2}+1}$+$\sqrt{(x+1)^{2}+4}$
=$\sqrt{(x-2)^{2}+(0-1)^{2}}$+$\sqrt{(x+1)^{2}+(0+2)^{2}}$,
表示x轴上一点P(x,0)到定点A(2,1),B(-1,-2)的距离,
由于A,B分别在x轴的两边,连接AB,
可得|AB|=$\sqrt{(2+1)^{2}+(1+2)^{2}}$=3$\sqrt{2}$.
则函数y=$\sqrt{{x}^{2}-4x+5}$+$\sqrt{{x}^{2}+2x+5}$的最小值为3$\sqrt{2}$.
点评 本题考查函数最值的求法,注意运用转化思想,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数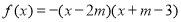 (其中
(其中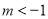 ),
),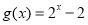 .
.
(1)若命题“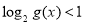 ”是真命题,求
”是真命题,求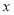 的取值范围;
的取值范围;
(2)设命题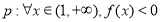 或
或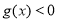 ;命题
;命题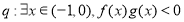 ,若
,若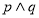 是真命题,求
是真命题,求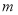 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.“ ”是“函数
”是“函数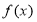 是奇函数”的充要条件
是奇函数”的充要条件
B.命题“若 ,则
,则 ”的否命题是“若
”的否命题是“若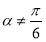 ,则
,则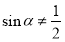 ”
”
C.若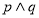 为假命题,则
为假命题,则 均为假命题
均为假命题
D.若 ,
, ,则
,则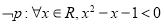
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
观察下列散点图,其中两个变量的相关关系判断正确的是( )
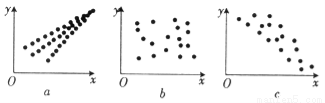
A. 为正相关,
为正相关,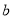 为负相关,
为负相关,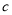 为不相关
为不相关
B.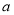 为负相关,
为负相关,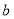 为不相关,
为不相关,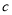 为正相关
为正相关
C.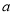 为负相关,
为负相关,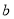 为正相关,
为正相关,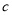 为不相关
为不相关
D.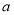 为正相关,
为正相关,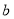 为不相关,
为不相关,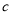 为负相关
为负相关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com