
分析 (1)利用f(x)>0的解集为{x|-3<x<4},得出a,b,c的关系,再解关于x的不等式bx2+2ax-(c+3b)<0.
(2)若对任意x∈R,不等式f(x)≥2ax+b恒成立,得出$\left\{\begin{array}{l}a>0\\△={({b-2a})^2}-4a({c-b})≤0\end{array}\right.?\left\{\begin{array}{l}a>0\\{b^2}+4{a^2}-4ac≤0\end{array}$,即可求${\;}_{\;}^{\;}\frac{b^2}{{{a^2}+{c^2}}}_{\;}^{\;}$的最大值.
解答 解:(1)∵ax2+bx+c>0的解集为{x|-3<x<4},
∴a<0,-3+4=-$\frac{b}{a},-3×4=\frac{c}{a}⇒b=-a,c=-12a({a<0})$.
∴bx2+2ax-(c+3b)<0?-ax2+2ax+15a<0(a<0)?x2-2x-15<0,
∴解集为(-3,5).
(2)∵f(x)≥2ax+b?ax2+(b-2a)x+c-b≥0恒成立,
∴$\left\{\begin{array}{l}a>0\\△={({b-2a})^2}-4a({c-b})≤0\end{array}\right.?\left\{\begin{array}{l}a>0\\{b^2}+4{a^2}-4ac≤0\end{array}$,
∴0≤b2≤4a(c-a),∴$\frac{b^2}{{{a^2}+{c^2}}}≤\frac{{4a({c-a})}}{{{a^2}+{c^2}}}=\frac{{4({\frac{c}{a}-1})}}{{1+{{({\frac{c}{a}})}^2}}}$
$令_{\;}^{\;}t=\frac{c}{a}$-1,∵4a(c-a)≥b2≥0,∴c≥a>0⇒$\frac{c}{a}$≥1⇒t≥0.
∴${\;}_{\;}^{\;}\frac{b^2}{{{a^2}+{c^2}}}_{\;}^{\;}$≤$\frac{4t}{1+(t+1)^{2}}$=$\frac{4t}{{t}^{2}+2t+2}$.
令g(t)=$\frac{4t}{{t}^{2}+2t+2}$(t≥0).
当t=0时,g(0)=0,当t>0时,g(t)=$\frac{4}{t+\frac{2}{t}+2}$≤$\frac{4}{2\sqrt{2}+2}$=2$\sqrt{2}$-2,
∴${\;}_{\;}^{\;}\frac{b^2}{{{a^2}+{c^2}}}_{\;}^{\;}$的最大值为2$\sqrt{2}$-2.
点评 本题考查不等式的解法,考查恒成立问题,考查学生转化问题的方法,属于中档题.


科目:高中数学 来源: 题型:填空题
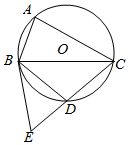 如图,A,B,C是⊙O上的三点,点D是劣弧$\widehat{BC}$的中点,过点B的切线交弦CD的延长线于点E.若∠BAC=80°,则∠BED=60°.
如图,A,B,C是⊙O上的三点,点D是劣弧$\widehat{BC}$的中点,过点B的切线交弦CD的延长线于点E.若∠BAC=80°,则∠BED=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a>b>c | C. | b<a<c | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com