
| A. | ①③④ | B. | ①④⑤ | C. | ②③④ | D. | ①②⑤ |
分析 根据已知中函数具有“自平行性”的定义,逐一分析5个函数是否具有“自平行性”,最后综合讨论结果,可得答案.
解答 解:函数f(x)具有“自平行性”,即对定义域内的任意自变量x1,总存在x2≠x1,使得f′(x1)=f′(x2).
对于①,f′(x)=cosx,具有周期性,必满足条件,故①正确;
对于②,f′(x)=3x2(-1≤x≤2),对任意x1∈(1,2],不存在x2≠x1,使得f′(x1)=f′(x2)成立,故②错误;
对于③,当x<0时,f′(x)=ex∈(0,1),而x>m时,f′(x)=1-$\frac{1}{{x}^{2}}$∈(0,1),解得x<-1(舍去),或x>1,则m=1,故③正确;
对于④,f(x)=x,(x≠0)不符合定义,故④正确;
对于⑤,同④,其导函数为奇函数,故⑤不正确.
故选:A.
点评 本题以命题的真假判断为载体,考查了函数具有“自平行性”的定义,正确理解函数具有“自平行性”的定义,是解答的关键.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
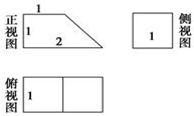
| A. | 7+$\sqrt{2}$ | B. | $\frac{11}{2}$+$\sqrt{2}$ | C. | 7+$\sqrt{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{x+4}-1(x>0)$ | B. | $\sqrt{x+4}-1(x>0)$ | C. | $-\sqrt{x+4}-1(x<-3)$ | D. | $\sqrt{x+4}-1(x<-3)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂直于同一条直线的两直线平行 | |
| B. | 垂直于同一条直线的两直线垂直 | |
| C. | 垂直于同一个平面的两直线平行 | |
| D. | 垂直于同一条直线的一条直线和平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com