
分析 (1)根据两角和的余弦定理和辅助角公式化简函数解析式,由正弦函数的对称中心求得函数图象的对称中心.
(2)根据正弦定理,化简$\frac{b}{c}$,再构造函数,利用函数的单调性即可求出.
解答 解:(1)$f(x)=2cos(2x+\frac{π}{3})-2cos2x+1$,
=-cos2x-$\sqrt{3}$sin2x+1,
=-2sin(2x+$\frac{π}{6}$)+1,
对称中心横坐标满足:2x+$\frac{π}{6}$=kπ,k∈Z,
∴x=-$\frac{π}{12}$+$\frac{k}{2}$π,
∴对称中心为(-$\frac{π}{12}$+$\frac{k}{2}$π,1)
(2)∵f(A)=0,
∴-2sin(2A+$\frac{π}{6}$)+1=0,
∴sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
∴2A+$\frac{π}{6}$=$\frac{5π}{6}$,
A=$\frac{π}{3}$,
∴B+C=$\frac{2π}{3}$
∵△ABC为锐角三角形
∴$\frac{b}{c}$=$\frac{sinB}{sinC}$=$\frac{\frac{\sqrt{3}}{2}cosC+\frac{1}{2}sinC}{sinC}$=$\frac{\sqrt{3}}{2}$$\frac{1}{tanC}$+$\frac{1}{2}$,
∵0<B<$\frac{π}{2}$,0<C<$\frac{π}{2}$
∴$\frac{π}{6}$<C<$\frac{π}{2}$
∴tanC>$\sqrt{3}$
∴$\frac{1}{tanC}$<$\frac{1}{\sqrt{3}}$
∴$\frac{1}{2}$<$\frac{b}{c}$<2
∴$\frac{b}{c}$的范围是($\frac{1}{2}$,2)
点评 本题考查三角函数的化简,两角和的正弦与余弦公式,正切函数的应用,正弦定理的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
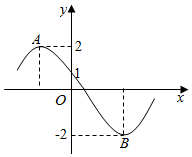 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么$\frac{f(-1)}{2}$=( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么$\frac{f(-1)}{2}$=( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{3}$ | B. | $-2-\sqrt{3}$ | C. | $-2+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
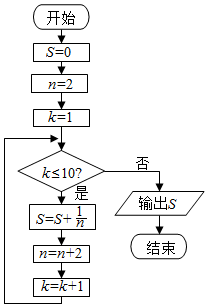
| A. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{11}$ | B. | $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{22}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{10}$ | D. | $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|α=k?360°+527°,k∈Z} | B. | { α|α=k?360°+157°,k∈Z } | ||
| C. | {α|α=k?360°+193°,k∈Z } | D. | { α|α=k?360°-193°,k∈Z } |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com