
【题目】已知函数![]() 满足:对任意
满足:对任意![]() ,
,![]() ,都有
,都有![]() ,则不等式
,则不等式![]() 的解集为________.
的解集为________.
科目:高中数学 来源: 题型:
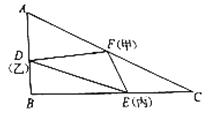
【题目】为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端,甲站在直角![]() 斜边
斜边![]() 的中点
的中点![]() 处,乙站在
处,乙站在![]() 处,丙站在
处,丙站在![]() 处.游戏开始,甲不动,乙、丙分别以
处.游戏开始,甲不动,乙、丙分别以![]() 和
和![]() 的速度同时出发,匀速跑向终点
的速度同时出发,匀速跑向终点![]() 和
和![]() ,运动过程中绷紧的橡皮带围成一个如图所示的
,运动过程中绷紧的橡皮带围成一个如图所示的![]() .(规定:只要有一人跑到终点,游戏就结束,且
.(规定:只要有一人跑到终点,游戏就结束,且![]() ).已知
).已知![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,记经过
,记经过![]() 后
后![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数表示,并求出
的函数表示,并求出![]() 的取值范围;
的取值范围;
(2)当游戏进行到![]() 时,体育教师宣布停止,求此时
时,体育教师宣布停止,求此时![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系中的坐标原点为极点,![]() 轴的正半抽为极轴,建立极坐标系,曲线
轴的正半抽为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于充分必要条件的判断中,错误的是( )
A.“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
B.“![]() ”是“
”是“![]() ”的必要条件
”的必要条件
C.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D.“![]() ,
,![]() ”是“
”是“![]() ”的非充分非必要条件
”的非充分非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次电影展,有14部参赛影片,组委会分两天在某一影院播映这14部电影,每天7部,其中有2部4D电影要求不在同一天放映,下列不能作为排片方案数的计算式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com