分析:(1)利用导数求出函数f(x)的图象在点(1,f(1))处的切线方程,再有直线与曲线的相切关系,联立方程组求出b的值;
(2)根据题意求满足条件的最大整数M,转化为求h(x)的最值解决,即只要使得M≤h(x)
max-h(x)
min即可;
(3)先利用导数法判断f(x)与g(x)的增减性,把|f(x
1)-f(x
2)|>|g(x
1)-g(x
2)|等价转化为f(x
1)-f(x
2)>g(x
2)-g(x
1),等价于f(x
1)+g(x
1)>f(x
2)+g(x
2)成立,再构造函数φ(x)=f(x)+g(x),即等价于φ(x)=f(x)+g(x)=lnx+
x2-bx+1 在区间[1,2]上是增函数,利用导数与函数单调性的关系,结合不等式恒成立的条件,求得b的取值范围.
解答:
解:(1)∵f(x)=lnx,∴f′(x)=
,f′(1)=1,
∴函数f(x)的图象在点(1,f(1))处的切线方程为y=x-1,----------------(2分)
∵直线y=x-1与函数g(x)的图象相切,由
消去y得x
2-2(b+1)x+4=0,
则△=4(b+1)
2-16=0,解得b=1或-3--------------------------------------(4分)
(2)当b=0时,∵h(x)=f(x)-g(x)=lnx-
x2-1 (x∈[1,2]),
∴h′(x)=
-x=
,----------------------------------------------(5分)
当x∈(1,2]时,h′(x)<0,∴在[1,2]上单调递减,
h(x)
max=h(1)=-
,h(x)
min=h(2)=ln2-3,-----------------------------------(7分)
则[h(x
1)-h(x
2)]
max=h(x)
max-h(x)
min=
-ln2,
∴M≤
-ln2<1,故满足条件的最大整数是M=0.------------------------------(9分)
(3)不妨设x
1>x
2,∵函数f(x)=lnx在区间[1,2]上是增函数,∴f(x
1)>f(x
2),
∵函数g(x)图象的对称轴为x=b,且b≥2,∴函数g(x)在区间[1,2]上是减函数,
∴g(x
1)<g(x
2),------------------------------------------------------(10分)
∴|f(x
1)-f(x
2)|>|g(x
1)-g(x
2)|等价于f(x
1)-f(x
2)>g(x
2)-g(x
1),
即f(x
1)+g(x
1)>f(x
2)+g(x
2),----------------------------------(11分)
等价于φ(x)=f(x)+g(x)=lnx+
x2-bx+1 在区间[1,2]上是增函数,
等价于φ′(x)=
+x+b≥0在区间[1,2]上恒成立,---------------------------(12分)
等价于b≤x+
在区间[1,2]上恒成立,
∴b≤2,又b≥2,∴b=2.------------------------------------------------(14分)



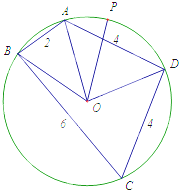 已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.
已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.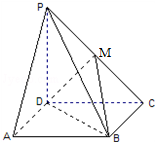 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点. 某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了n人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了n人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示: