
分析 (1)求导,由题意可得f'(1)=1,代入即可求得a的值;
(2)由题意可知:4lnx≤m(3x-$\frac{1}{x}$-2)恒成立,构造辅助函数,求导,分类讨论即可求出m的取值范围
解答 解:(1)f′(x)=$\frac{(\frac{4x+a}{x}+4lnx)(3x+1)-3(4x+a)lnx}{(3x+1)^{2}}$
由题设f′(1)=1,
∴$\frac{4+a}{4}=1$,
∴a=0.
(2)$f(x)=\frac{4xlnx}{3x+1}$,?x∈[1,+∞),f(x)≤m(x-1),即4lnx≤m(3x-$\frac{1}{x}$-2)
设g(x)=4lnx-m(3x-$\frac{1}{x}$-2),即?x∈[1,|+∞),g(x)≤0,
∴g′(x)=$\frac{4}{x}$-m(3+$\frac{1}{{x}^{2}}$)=$\frac{-3m{x}^{2}+4x-m}{{x}^{2}}$,g′(1)=4-4m
①若m≤0,g′(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾
②若m∈(0,1),当x∈(1,$\frac{2+\sqrt{4-3{m}^{2}}}{3m}$),g′(x)>0,g(x)单调递增,g(x)≥g(1)=0,与题设矛盾.
③若m≥1,当x∈(1,+∞),),g′(x)≤0,g(x)单调递减,g(x)≤g(1)=0,即不等式成立
综上所述,m≥1.
点评 本题考查导数的综合应用,导数的几何意义,考查导数与函数的单调性和最值的关系,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
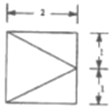 己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )
己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )| A. | 8π | B. | 12π | C. | 4π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}f(2)<f(1)$ | B. | $\frac{2}{e}f(2)>f(1)$ | C. | f(1)>0 | D. | f(-1)>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com