
分析 (1)要使函数过定点,则需a的系数3x2-4x+1为0,解得x=1或x=$\frac{1}{3}$.
(2)先对a进行分类讨论,再对对称轴进行分类.
解答 (1)∵a+b=1,∴b=1-a.
∴f(x)=a(3x2-4x+1)-1,
要使函数过定点,则需3x2-4x+1=0,
解得x=1或x=$\frac{1}{3}$.
故可知函数的图象必过的定点是(1,-1)和($\frac{1}{3}$,-1).
(2)当a=0时,f(x)=2(b-1)x-b∈[b-2,2-3b],所以此时|f(x)|≤5;
当a<0时,对称轴x=$\frac{a-b+1}{3a}≤\frac{1}{3}$,
①$\frac{a-b+1}{3a}≤-1$,即b≤1+4a时,f(x)∈[a+b-2,5a-3b+2],此时-4≤f(x)≤5,
②$\frac{a-b+1}{3a}>-1$,即b>1+4a时,f(x)≤-b-$\frac{(a-b+1)^{2}}{3a}$<-b-3a≤4,
又f(x)≥min{a-b+2,5a-3b+2}≥-6,所以|f(x)|≤6,
当a>0时,对称轴x=$\frac{a-b+1}{3a}$≥$\frac{1}{3}$
$①\frac{a-b+1}{3a}≥1,即b≤1-2a时$,f(x)≤5a-3b+2≤10,
f(x)≥a+b-2≥-3,所以|f(x)|≤10.
$②\frac{a-b+1}{3a}<1,即b>1-2a时$,f(x)≤5a-3b+2≤10.
f(x)≥-b-$\frac{(a-b+1)^{2}}{3a}$≥-b-3a≥4,所以|f(x)|≤10.
综上,M的最大值为10,当a=1,b=-1,x=-1时取到.
点评 本题考查函数过定点问题和分类讨论.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
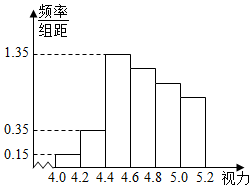 某学校研究性学习小组对该校高二学生视力情况进行调查,在高二的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图:
某学校研究性学习小组对该校高二学生视力情况进行调查,在高二的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图:| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{7}{4}$,$\frac{23}{4}$) | B. | (-∞,$\frac{23}{4}$) | C. | (-$\frac{7}{4}$,6) | D. | (-2,$\frac{23}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,1 | B. | 0,2 | C. | 1,2 | D. | 1,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com