
分析 根据题干条件求出a1+2a2+22a3+…+2n-2an-1=(n-1)2,与题干等式相减即可求出数列{an}的表达式.
解答 解:∵a1+2a2+22a3+…+2n-1an=n2…①,
∴a1+2a2+22a3+…+2n-2an-1=(n-1)2…②,
①-②得2n-1an=2n-1,
∴an=$\frac{2n-1}{{2}^{n-1}}$,
当n=1时,a1=$\frac{1}{1}$=1=12,
∴an=$\frac{2n-1}{{2}^{n-1}}$,
故答案为:$\frac{2n-1}{{{2^{n-1}}}}$
点评 本题主要考查数列递推式的知识点,解答本题的关键是求出a1+2a2+22a3+…+2n-2an-1=(n-1)2,此题比较简单.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
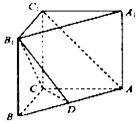 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-2或a=1 | B. | a≤2或1≤a≤2 | C. | a≥1 | D. | -2≤a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com