某商场销售某种商品的经验表明，该商品每日的销售量
（单位：千克）与销售价格
（单位：元/千克）满足关系式
其中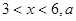
为常数。己知销售价格为5元/千克时，每日可售出该商品11千克。
（1）求
的值；
（2）若该商品的成本为3元/千克，试确定销售价格的值，使商场每日销售该商品所获得的利润最大。
（1）
（2）
时，函教
取得最大值，且最大值为42.
解析试题分析：（1）将
代入计算即得所求.
（2）依题意，该商品每日的销售量
，
所以商场每日销售该商品所获得利润
利用导数，通过“求导数、求驻点、讨论区间导数值符号、确定极值、比较区间端点函数值、确定最值”.
利用“表解法”，形象直观，易于理解.
试题解析：（1）因为时，
。所以
3分
（2）由（1）可知，该商品每日的销售量，
所以商场每日销售该商品所获得利润 7分
从而
9分
于是，当变化时，
，的变化情况如下表
由表知，（3,4） 4 （4,6） +[ 0 — 单调递增 极大值42 单调递减 是函数在区间
内的极大值点，也是最大值点。
所以当时，函教取得最大值，且最大值为42 12分
考点：生活中的优化问题举例，利用导数研究函数的最值.
名校课堂系列答案科目：高中数学 来源： 题型：解答题
设函数f（x）定义在（0，+∞）上，f（1）=0，导函数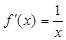
，
.
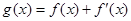（1）求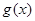
的单调区间和最小值；
（2）讨论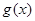与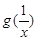
的大小关系；
（3）是否存在x0＞0，使得|g（x）﹣g（x0）|＜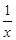
对任意x＞0成立？若存在，求出x0的取值范围；若不存在请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝2ax－
－(2＋a)lnx(a≥0).
（1）当a＝0时，求f(x)的极值；
（2）当a＞0时，讨论f(x)的单调性；
（3）若对任意的a∈(2,3)，x1,x2∈[1,3]，恒有(m－ln3)a－2ln3＞|f(x1)－f(x2)|成立，求实数m的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（满分12分）已知函数
.
（1）当
时，求函数
的单调区间；
（2）若函数在区间
上为减函数，求实数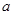
的取值范围；
（3）当
时，不等式
恒成立，求实数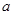的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知二次函数
，关于x的不等式
的解集为
，其中m为非零常数.设
.
(1)求a的值；
(2)
如何取值时，函数
存在极值点，并求出极值点；
(3)若m=1，且x>0，求证：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
的单调区间；
时，求证：
恒成立..
．
，求曲线
在点
处的切线方程； 
求函数
的单调区间.
与直线
，
，
所围成平面图形的面积.
，函数
是区间
上的减函数.
的最大值；
恒成立，求
的取值范围；
的方程
的根的个数．