
已知 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 求函数
求函数 的单调区间.
的单调区间.
(1)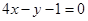 ;(2)当
;(2)当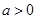 时,
时, 的单调递减区间为
的单调递减区间为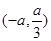 ,单调递增区间为
,单调递增区间为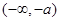 ,
,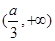 ;当
;当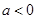 时,
时, 的单调递减区间为
的单调递减区间为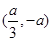 ,单调递增区间为
,单调递增区间为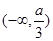 ,
,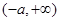 .
.
解析试题分析:(1)当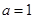 时,先求出
时,先求出 ,根据导数的几何意义可得切线的斜率
,根据导数的几何意义可得切线的斜率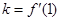 ,进而计算出
,进而计算出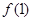 确定切点坐标,最后由点斜式即可写出切线的方程并化成直线方程的一般式;(2)先求导并进行因式分解
确定切点坐标,最后由点斜式即可写出切线的方程并化成直线方程的一般式;(2)先求导并进行因式分解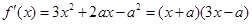 ,求出
,求出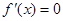 的两个解
的两个解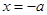 或
或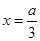 ,针对两根的大小进行分类讨论即分
,针对两根的大小进行分类讨论即分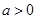 、
、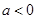 两类进行讨论,结合二次函数的图像与性质得出函数
两类进行讨论,结合二次函数的图像与性质得出函数 的单调区间,最后再将所讨论的结果进行阐述,问题即可解决.
的单调区间,最后再将所讨论的结果进行阐述,问题即可解决.
试题解析:(1) ∵ 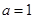 ∴
∴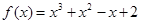 ∴
∴  2分
2分
∴ 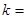
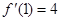 , 又
, 又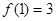 ,所以切点坐标为
,所以切点坐标为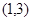
∴ 所求切线方程为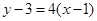 ,即
,即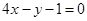 5分
5分
(2)
由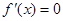 得
得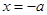 或
或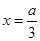 7分
7分
①当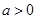 时,由
时,由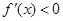 , 得
, 得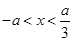 ,由
,由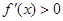 , 得
, 得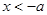 或
或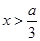 9分
9分
此时 的单调递减区间为
的单调递减区间为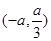 ,单调递增区间为
,单调递增区间为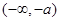 和
和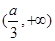 10分
10分
②当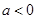 时,由
时,由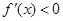 ,得
,得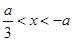 ,由
,由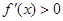 ,得
,得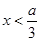 或
或 12分
12分
此时 的单调递减区间为
的单调递减区间为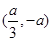 ,单调递增区间为
,单调递增区间为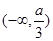 和
和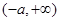 13分
13分
综上:当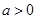 时,
时, 的单调递减区间为
的单调递减区间为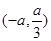 ,单调递增区间为
,单调递增区间为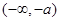 ,
,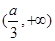 ;当
;当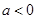 时,
时, 的单调递减区间为
的单调递减区间为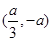 单调递增区间为
单调递增区间为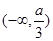 ,
,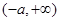 14分.
14分.
考点:1.导数的几何意义;2.函数的单调性与导数;3.分类讨论的思想.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
设函数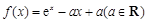 ,其图象与
,其图象与 轴交于
轴交于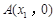 ,
, 两点,且x1<x2.
两点,且x1<x2.
(1)求 的取值范围;
的取值范围;
(2)证明: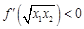 (
( 为函数
为函数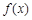 的导函数);
的导函数);
(3)设点C在函数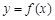 的图象上,且△ABC为等腰直角三角形,记
的图象上,且△ABC为等腰直角三角形,记 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中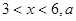 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数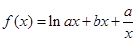 (
( 、
、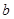 为常数),在
为常数),在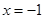 时取得极值.
时取得极值.
(1)求实数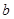 的取值范围;
的取值范围;
(2)当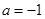 时,关于
时,关于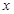 的方程
的方程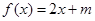 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数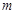 的取值范围;
的取值范围;
(3)数列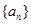 满足
满足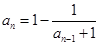 (
(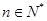 且
且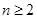 ),
),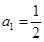 ,数列
,数列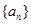 的前
的前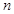 项和为
项和为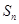 ,
,
求证: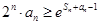 (
(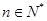 ,
,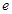 是自然对数的底).
是自然对数的底).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com