
已知函数f(x)=2ax- -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2,3),x1,x2∈[1,3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围。
(1)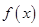 的极大值为
的极大值为 ,无极小值.(3)
,无极小值.(3)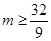
解析试题分析:(1)求已知函数的极值,利用导数法,即求定义域,求导,求导数为0与单调区间,判断极值点求出极值. (2) 求定义域,求导.利用数形结合思想讨论导数(含参数二次不等式)的符号求f(x)的单调区间,讨论二次含参数不等式注意按照定性(二次项系数是否为0),开口,判别式,两根大小得顺序依次进行讨论,进而得到函数f(x)的单调性(注意单调区间为定义域的子集)(3)这是一个恒成立问题,只需要(m-ln3)a-2ln3>(|f(x1)-f(x2)|) ,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|)
,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|) =
=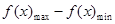 ,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|)
,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|) . (m-ln3)a-2ln3>(|f(x1)-f(x2)|)
. (m-ln3)a-2ln3>(|f(x1)-f(x2)|) 对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.
对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.
试题解析:(1)当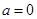 时,
时,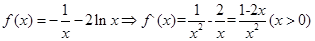 ,由
,由 ,解得
,解得 ,可知
,可知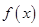 在
在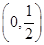 上是增函数,在
上是增函数,在 上是减函数.
上是减函数.
∴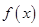 的极大值为
的极大值为 ,无极小值.
,无极小值.
①当 时,
时,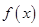 在
在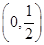 和
和 上是增函数,在
上是增函数,在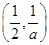 上是减函数;
上是减函数;
②当 时,
时,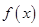 在
在 上是增函数;
上是增函数;
③当 时,
时,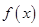 在
在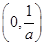 和
和 上是增函数,在
上是增函数,在 上是减函数 8分
上是减函数 8分
(3)当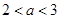 时,由(2)可知
时,由(2)可知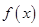 在
在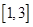 上是增函数,
上是增函数,
∴ .
.
由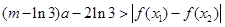 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
∴
即 对任意
对任意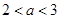 恒成立,
恒成立,
即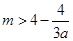 对任意
对任意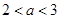 恒成立,由于当
恒成立,由于当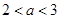 时,
时, ,∴
,∴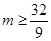 .
.
考点: 导数 恒成立问题 不等式


科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中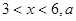 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量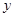 (升)与行驶速度
(升)与行驶速度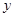 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com