
分析 (1)代入b值,不等式可因式分解为(ax-1)(x-1)<0,对参数a分类讨论,得出解集;
(2)由条件可知2a+b+ab=4,由不等式性质$ab≤\frac{1}{2}•{(\frac{2a+b}{2})^2}$,可得$4≤2a+b+\frac{{{{(2a+b)}^2}}}{8}$,利用换元法解不等式即可.
解答 解:(1)当b=1时,f(x)=ax2-(a+1)x+1=(ax-1)(x-1),
所以(ax-1)(x-1)<0.
①当a=0时,此不等式解集为{x|x>1}
②当a<0时,此不等式解集为$\{x\left|{x<\frac{1}{a}或x>1\}}\right.$
当a>0时,
若$\frac{1}{a}>1$即0<a<1时,此不等式解集为$\{x\left|{1<x<\frac{1}{a}\}}\right.$;
若$\frac{1}{a}=1$即a=1时,此不等式解集为∅;
若$\frac{1}{a}<1$即a>1时,此不等式解集为$\{x\left|{\frac{1}{a}<x<1\}}\right.$.…(6分)
(2)f(-2)=4a+2ab+2b+1=9得:2a+b+ab=4,
∵$ab≤\frac{1}{2}•{(\frac{2a+b}{2})^2}$,
∴$4≤2a+b+\frac{{{{(2a+b)}^2}}}{8}$,
解得:$2a+b≥4({\sqrt{3}-1})$($2a+b≤-4\sqrt{3}-4$(舍去))
当且仅当2a=b,即$a=\sqrt{3}-1,b=2\sqrt{3}-2$时上式取等号.
所以2a+b的最小值为$4\sqrt{3}-4$.…(12分)
点评 考查了二次不等式解集的分类讨论问题,不等式的证明,难点是对常用不等式$ab≤\frac{1}{2}•{(\frac{2a+b}{2})^2}$的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
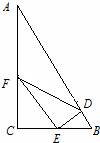 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | $\frac{1}{21}$ | C. | 16 | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com