
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
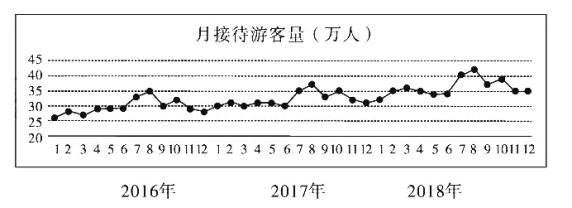
根据该折线图,判断下列结论:
(1)月接待游客量逐月增加;
(2)年接待游客量逐年增加;
(3)各年的月接待游客量高峰期大致在7,8月;
(4)各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳.
其中正确结论的个数为( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() _____.
_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
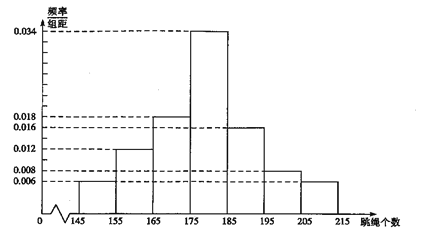
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com