
分析 (Ⅰ)求出函数g(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数在(0,2)的最大值和最小值,求出a的范围即可;
(Ⅱ)根据函数f(x)的定义域为(0,+∞),得到函数在定义域内的最小值为1,则答案得证.
解答 (Ⅰ)解:g′(x)=$\frac{1-x}{{e}^{x}}$,
令g′(x)>0,解得:x<1,令g′(x)<0,解得:x>1,
故g(x)在(0,1)递增,在(1,2)递减,
故g(x)max=g(1)=$\frac{1}{e}$,而g(0)=0,g(2)=$\frac{2}{{e}^{2}}$,
若g(x)=a在(0,2)上有两个不等实根,
则$\frac{2}{{e}^{2}}$<a<$\frac{1}{e}$;
(Ⅱ)证明:要证明f(x)+$\frac{2}{eg(x)}$>0,
即证明xln x>xe-x-$\frac{2}{e}$
设函数m(x)=xln x,
则m′(x)=1+ln x,
所以当x∈(0,$\frac{1}{e}$)时,m′(x)<0;
当x∈($\frac{1}{e}$,+∞)时,m′(x)>0.
故m(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,
从而m(x)在(0,+∞)上的最小值为m($\frac{1}{e}$)=-$\frac{1}{e}$,
设函数n(x)=xe-x-$\frac{2}{e}$,则n′(x)=e-x(1-x).
所以当x∈(0,1)时,n′(x)>0;
当x∈(1,+∞)时,n′(x)<0.
故n(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
从而n(x)在(0,+∞)上的最大值为n(1)=-$\frac{1}{e}$;
因为mmin(x)=m(1)=nmax(x),
所以当x>0时,m(x)>n(x),
即f(x)+$\frac{2}{eg(x)}$>0.
点评 本题考查了导数的应用,考查函数的单调性问题,考查了利用导数求函数的最值,是中高档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
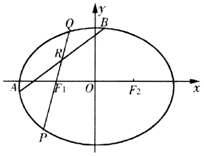 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
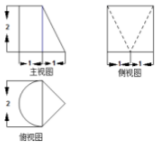
| A. | π+$\frac{4}{3}$ | B. | $\frac{π}{3}$+4 | C. | $\frac{2}{3}$π+$\frac{4}{3}$ | D. | $\frac{2}{3}$π+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
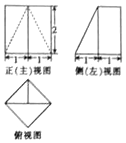 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{32}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | ?-$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com