
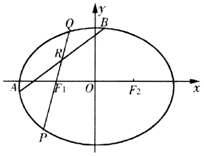
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.分析 (I)将点代入椭圆方程,由函数的对称性求得a=2c,即可求得椭圆的标准方程;
(II)由圆D,求得圆心坐标,利用点差法,求得直线AB的方程,代入椭圆方程,求得A,B点坐标,求得F1R的斜率的取值范围,则设F1R的方程y=k(x+1),代入椭圆方程,由韦达定理及$|{P{F_1}}|=\sqrt{1+{k^2}}|{{x_3}+1}|$,$|{Q{F_1}}|=\sqrt{1+{k^2}}|{{x_4}+1}|$,即可求得|PF1||QF1|的取值范围.
解答 解:(Ⅰ)∵椭圆C过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,
∴$\frac{3}{a^2}+\frac{3}{{4{b^2}}}=1$,①
∵椭圆C关于直线x=c对称的图形过坐标原点,∴a=2c,
∵a2=b2+c2,∴${b^2}=\frac{3}{4}{a^2}$,②
由①②得a2=4,b2=3,
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)因为AB为圆D的直径,所以点D:$(-\frac{{4\sqrt{3}}}{7},\frac{{3\sqrt{3}}}{7})$为线段AB的中点,
设A(x1,y1),B(x2,y2),则,$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{{8\sqrt{3}}}{7}\\{y_1}+{y_2}=\frac{{6\sqrt{3}}}{7}\end{array}\right.$,又$\begin{array}{l}\left\{\begin{array}{l}\frac{{{x_1}^2}}{4}+\frac{{{y_1}^2}}{3}=1\\ \frac{{{x_2}^2}}{4}+\frac{{{y_2}^2}}{3}=1\end{array}\right.\end{array}$,
所以$\frac{{({x_1}+{x_2})({x_1}-{x_2})}}{4}+\frac{{({y_1}+{y_2})({y_1}-{y_2})}}{3}=0$,则(x1-x2)-(y1-y2)=0,故${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=1$,
则直线AB的方程为$y-\frac{{3\sqrt{3}}}{7}=x+\frac{{4\sqrt{3}}}{7}$,即$y=x+\sqrt{3}$,…(7分)
代入椭圆C的方程并整理得$7{x^2}+8\sqrt{3}x=0$,则${x_1}=-\frac{{8\sqrt{3}}}{7},{x_2}=0$,
故直线F1R的斜率$k∈[{\sqrt{3},+∞})$.
设F1R:y=k(x+1),由$\left\{\begin{array}{l}y=k(x+1)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3+4k2)x2+8k2x+4k2-12=0,
设P(x3,y3),Q(x4,y4),则有${x_3}+{x_4}=\frac{{-8{k^2}}}{{3+4{k^2}}}$,${x_3}{x_4}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$.
又$|{P{F_1}}|=\sqrt{1+{k^2}}|{{x_3}+1}|$,$|{Q{F_1}}|=\sqrt{1+{k^2}}|{{x_4}+1}|$,…(10分)
所以|PF1||QF1|=(1+k2)|x3x4+(x3+x4)+1|=$(1+{k^2})\frac{9}{{3+4{k^2}}}=\frac{9}{4}(1+\frac{1}{{3+4{k^2}}})$,
因为$k≥\sqrt{3}$,所以$\frac{9}{4}<\frac{9}{4}(1+\frac{1}{{3+4{k^2}}})≤\frac{12}{5}$,
即|PF1||QF1|的取值范围是$({\frac{9}{4},\frac{12}{5}}]$.…(13分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理及弦长公式的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | e | C. | 3 | D. | 2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
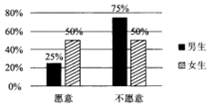 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 15 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com