
| A. | 2 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2+\sqrt{2}$ |
分析 由S2017-a1=(a2+a3)+(a4+a5)+…+(a2016+a2017),结合余弦函数值求和,再由S2017+m=1010,可得a1+m=2,由a1•m>0,可得a1>0,m>0,运用乘1法和基本不等式即可得到所求最小值.
解答 解:数列{an}满足${a_{n+1}}+{a_n}=(n+1)•cos\frac{nπ}{2}(n≥2,n∈{N^*})$,
可得a2+a3=3cosπ=-3,a4+a5=5cos2π=5,a6+a7=7cos3π=-7,
…,a2016+a2017=2017cos1008π=2017,
则S2017-a1=(a2+a3)+(a4+a5)+…+(a2016+a2017)=-3+5-7+9-…+2017=1008,
又S2017+m=1010,
所以a1+m=2,
由a1•m>0,可得a1>0,m>0,
则$\frac{1}{a_1}+\frac{1}{m}$=$\frac{1}{2}$(a1+m)($\frac{1}{a_1}+\frac{1}{m}$)=$\frac{1}{2}$(2+$\frac{m}{{a}_{1}}$+$\frac{{a}_{1}}{m}$)≥$\frac{1}{2}$(2+2$\sqrt{\frac{m}{{a}_{1}}•\frac{{a}_{1}}{m}}$)=2.
当且仅当a1=m=1时,取得最小值2.
故选:A.
点评 本题考查数列与三角函数的结合,注意运用整体思想和转化思想,考查最值的求法,注意运用乘1法和基本不等式,考查运算能力,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
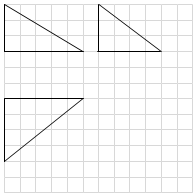 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )| A. | 25π | B. | 50π | C. | 75π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
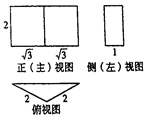
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
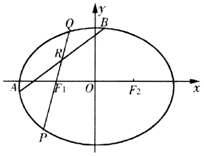 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
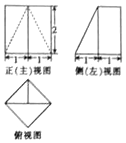 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{32}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com