
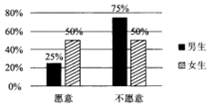
 2017��1��1�գ���Ϊ�����д��조ǧ֮�ǡ�27��ʾ���Թ�Ԫ֮һ��Ȫ������ʽ����Ԫ���ڼ䣬Ϊ�˻�Ծ���գ����췽������ˮ����ս��Ŀ��ȫ�����ţ��ִӵ��������������������ȡ��60��������40��Ů����100�˽��е��飬ͳ�Ƴ�100��������Ը�������ս�Ͳ�Ը�������ս����Ů���������������������ͼ����
2017��1��1�գ���Ϊ�����д��조ǧ֮�ǡ�27��ʾ���Թ�Ԫ֮һ��Ȫ������ʽ����Ԫ���ڼ䣬Ϊ�˻�Ծ���գ����췽������ˮ����ս��Ŀ��ȫ�����ţ��ִӵ��������������������ȡ��60��������40��Ů����100�˽��е��飬ͳ�Ƴ�100��������Ը�������ս�Ͳ�Ը�������ս����Ů���������������������ͼ����| Ը�� | ��Ը�� | �ܼ� | |
| ���� | |||
| �� | |||
| �ܼ� |
| P��K2��k0�� | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
���� ��1������k2���㹫ʽ���ɵó���
��2��������ɵã�X=0��1��2��ͨ���������ۣ�����������뻥���¼����ʼ��㹫ʽ���ɵó���
��� �⣺��1����ͳ�Ʊ���ɵã�
| Ը�� | ��Ը�� | �ܼ� | |
| ���� | 15 | 45 | 60 |
| �� | 20 | 20 | 40 |
| �ܼ� | 35 | 65 | 100 |
| X | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{3}{16}$ | $\frac{9}{16}$ |
���� ���⿼������������ķֲ��е����ʼ�����ѧ�������������Լ��顱���㹫ʽ����ԭ����������������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �й��ļ�����λ�����ݵ�4000����ǰ���������ĩ�ڣ���Ԫǰ221�꣬����ͳһ�й��䲼ͬһ�������گ�鲢�Ʒ��˳���Ȩ���������������ͼ�ǹŴ���һ�ֶ������ߡ��������ǣ���������ȣ�������ͼ��������ͼ�Ͳ���ͼΪ�������Σ�����ˡ����������Ϊ����λ���������ף���������
�й��ļ�����λ�����ݵ�4000����ǰ���������ĩ�ڣ���Ԫǰ221�꣬����ͳһ�й��䲼ͬһ�������گ�鲢�Ʒ��˳���Ȩ���������������ͼ�ǹŴ���һ�ֶ������ߡ��������ǣ���������ȣ�������ͼ��������ͼ�Ͳ���ͼΪ�������Σ�����ˡ����������Ϊ����λ���������ף���������| A�� | 2000 | B�� | 2800 | C�� | 3000 | D�� | 6000 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
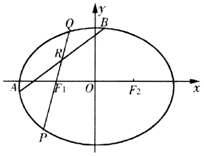 ��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$����$��{\sqrt{3}��\frac{{\sqrt{3}}}{2}}��$�����ҽ���ΪF1��-c��0����F2��c��0��������ԲC����ֱ��x=c�ԳƵ�ͼ�ι�����ԭ�㣮
��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$����$��{\sqrt{3}��\frac{{\sqrt{3}}}{2}}��$�����ҽ���ΪF1��-c��0����F2��c��0��������ԲC����ֱ��x=c�ԳƵ�ͼ�ι�����ԭ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
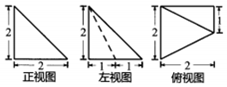 ijһ�ռ伸���������ͼ��ͼ��ʾ����ü��������ⳤΪ��������
ijһ�ռ伸���������ͼ��ͼ��ʾ����ü��������ⳤΪ��������| A�� | 2 | B�� | $\sqrt{5}$ | C�� | 2$\sqrt{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
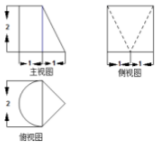
| A�� | ��+$\frac{4}{3}$ | B�� | $\frac{��}{3}$+4 | C�� | $\frac{2}{3}$��+$\frac{4}{3}$ | D�� | $\frac{2}{3}$��+4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮
��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{10}}{2}$ | B�� | $\frac{\sqrt{10}}{5}$ | C�� | $\sqrt{10}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com