
分析 若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),即存在x∈[1,2],使得g(x)=x2-2ax+4≤-1,即x2-2ax+5≤0,解得实数a的取值范围.
解答 (本小题满分12分)
解:由于f′(x)=1+$\frac{1}{(x+1)2}$>0,因此函数f(x)在[0,1]上单调递增,
所以x∈[0,1]时,f(x)min=f(0)=-1.
根据题意可知存在x∈[1,2],
使得g(x)=x2-2ax+4≤-1,即x2-2ax+5≤0,即a≥$\frac{x}{2}$+$\frac{5}{2x}$能成立,
令h(x)=$\frac{x}{2}$+$\frac{5}{2x}$,则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min,
又函数h(x)=$\frac{x}{2}$+$\frac{5}{2x}$在x∈[1,2]上单调递减,
所以h(x)min=h(2)=$\frac{9}{4}$,故只需a≥$\frac{9}{4}$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 21 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
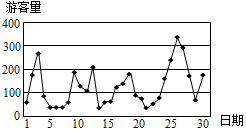 已知国家某5A级大型景区对拥挤等级与每日游客数量n(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
已知国家某5A级大型景区对拥挤等级与每日游客数量n(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:| 游客数量 (单位:百人) | [0,100) | [100,200) | [200,300) | [300,400] |
| 天数 | a | 10 | 4 | 1 |
| 频率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com