考点:数列与不等式的综合,等差关系的确定
专题:计算题,等差数列与等比数列,不等式的解法及应用
分析:(1)运用数列的通项和前n项和的关系,化简整理,即可得到
-=
,再由等差数列的定义,即可得到;
(2)运用等差数列的通项公式,注意n=1的情况,即可得到通项;
(3)求出数列b
n=
,考虑T
n+1-T
n,化简整理得到大于0,有n≥2时,T
2取得最小值,求出最小值,令m小于它即可.
解答:
解:(1)当n≥2时,2a
n=a
nS
n-S
n2,a
n=S
n-S
n-1,
即有2(S
n-S
n-1)=S
n(S
n-S
n-1)-S
n2=-S
nS
n-1.
则有
-=
,
则数列
{}为等差数列,且首项为1,公差为
;
(2)由等差数列的通项公式可得,
=1
+(n-1)=
,
即有S
n=
,
当n=1时,a
1=1,当n>1时,a
n=S
n-S
n-1=
-=
则a
n=
;
(3)b
n=
,即为b
n=
则T
n=
+
+…+
=
++…+
,
T
n+1=
++…+
++,
T
n+1-T
n=
++
-
-
=
-
>0,
即有n≥2时,T
2取得最小值,
则若T
n>m对n≥2恒成立可化为T
2>m,
又∵T
2=
+=
,
则m<
.
点评:本题考查数列的通项和前n项和的关系,考查等差数列的通项公式,考查数列的单调性和运用:解决恒成立问题,考查运算能力,属于中档题和易错题.



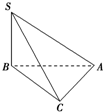 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: