
 如图,A、B是海岸线OM、ON上的两个码头,海中小岛有码头Q到海岸线OM、ON的距离分别为2km、$\frac{7\sqrt{10}}{5}$km.测得tan∠MON=-3,OA=6km.以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系.一艘游轮以18$\sqrt{2}$km/小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线AB经过Q).
如图,A、B是海岸线OM、ON上的两个码头,海中小岛有码头Q到海岸线OM、ON的距离分别为2km、$\frac{7\sqrt{10}}{5}$km.测得tan∠MON=-3,OA=6km.以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系.一艘游轮以18$\sqrt{2}$km/小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线AB经过Q).分析 (1)由已知得:A(6,0),直线ON的方程为y=-3x,求出Q(4,2),得直线AQ的方程,从而求出水上旅游线AB的长,由此能求出游轮在水上旅游线自码头A沿$\overrightarrow{AB}$方向开往码头B共航行时间.
(2)点P到直线AB的垂直距离最近,则垂足为C,分别求出直线AB的方程和直线PC的方程,联立直线AB和直线PC的方程组,能求出点C的坐标.
解答 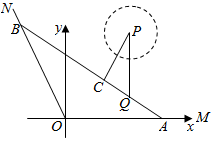 解:(1)由已知得:A(6,0),直线ON的方程为y=-3x,…1分
解:(1)由已知得:A(6,0),直线ON的方程为y=-3x,…1分
设Q(x1,2),(x1>0),由$\frac{|3{x}_{1}+2|}{\sqrt{10}}=\frac{7\sqrt{10}}{5}$及x1>0,得x1=4,∴Q(4,2),…3分
∴直线AQ的方程为y=-(x-6),即x+y-6=0,…5分
由$\left\{\begin{array}{l}{y=-3x}\\{x+y-6=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-3}\\{y=9}\end{array}\right.$,即B(-3,9),…6分
∴AB=$\sqrt{(-3-6)^{2}+{9}^{2}}$=9$\sqrt{2}$,即水上旅游线AB的长为9$\sqrt{2}$km.
游轮在水上旅游线自码头A沿$\overrightarrow{AB}$方向开往码头B共航行30分钟时间. …8分
(2)点P到直线AB的垂直距离最近,则垂足为C. …10分
由(1)知直线AB的方程为x+y-6=0,
P(4,8),则直线PC的方程为x-y+4=0,…12分
联立直线AB和直线PC的方程组$\left\{\begin{array}{l}{x+y-6=0}\\{x-y+4=0}\end{array}\right.$,
得点C的坐标为C(1,5). …14分
点评 本题考查直线与圆的位置关系在生产生活中的实际应用,是中档题,解题时要认真审题,注意圆的性质、直线方程的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=$\sqrt{2}$,AA′=1,点M,N分别为A′B和B′C′的中点.
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=$\sqrt{2}$,AA′=1,点M,N分别为A′B和B′C′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
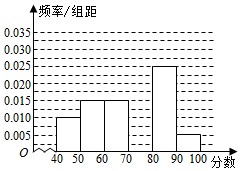 某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.
某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
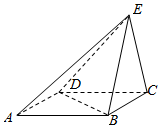 已知四棱锥E-ABCD的底面是平行四边形,BC=2,BD=$\sqrt{6}$,ED=4,EB=EC=$\sqrt{10}$,平面BCE⊥平面ABCD.
已知四棱锥E-ABCD的底面是平行四边形,BC=2,BD=$\sqrt{6}$,ED=4,EB=EC=$\sqrt{10}$,平面BCE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com