
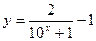 (x
(x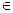 R)的反函数,函数g(x)的图象与函数
R)的反函数,函数g(x)的图象与函数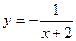 的图象关于直线x=-2成轴对称图形,设F(x)=f(x)+g(x).
的图象关于直线x=-2成轴对称图形,设F(x)=f(x)+g(x). 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形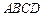 和
和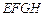 构成的面积为200
构成的面积为200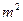 的十字型地域,计划在正方形
的十字型地域,计划在正方形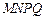 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元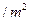 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元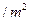 ,再在四个空角(如
,再在四个空角(如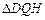 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元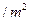 .设
.设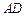 长为
长为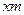 ,
,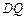 长为
长为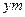 .
.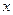 与
与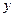 满足的等量关系式;
满足的等量关系式;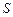 元,试建立
元,试建立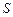 与
与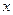 的函数关系;
的函数关系;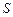 不超过138000元,求
不超过138000元,求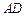 长
长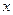 的取值范围.
的取值范围.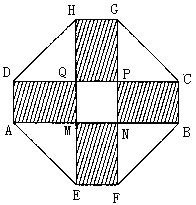
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
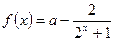 且满足
且满足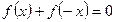 。
。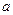 的值;
的值;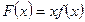 ,判别
,判别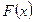 的符号且说明理由;
的符号且说明理由;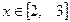 时,关于
时,关于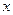 的方程
的方程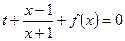 有实数解,求实数
有实数解,求实数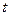 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com