
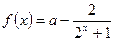 且满足
且满足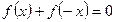 。
。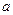 的值;
的值;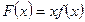 ,判别
,判别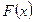 的符号且说明理由;
的符号且说明理由;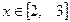 时,关于
时,关于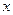 的方程
的方程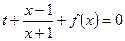 有实数解,求实数
有实数解,求实数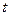 的取值范围。
的取值范围。 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源:不详 题型:解答题
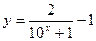 (x
(x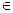 R)的反函数,函数g(x)的图象与函数
R)的反函数,函数g(x)的图象与函数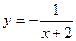 的图象关于直线x=-2成轴对称图形,设F(x)=f(x)+g(x).
的图象关于直线x=-2成轴对称图形,设F(x)=f(x)+g(x).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
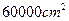 ,四周空白的宽度为
,四周空白的宽度为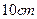 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为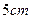 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: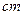 ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.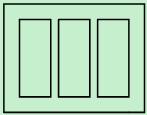
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
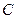 ,公路
,公路 恰好是
恰好是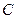 的准线,
的准线,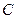 上的点
上的点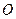 到
到 的距离最近,且为
的距离最近,且为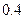 千米,城镇
千米,城镇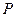 位于点
位于点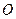 的北偏东
的北偏东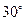 处,
处,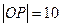 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路 以便建立水陆交通网.
以便建立水陆交通网.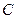 的方程;
的方程;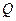 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)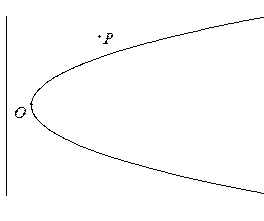
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
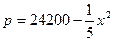 ,
,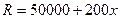 (元)。
(元)。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com