
 已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F
已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F分析 (I)根据A,B,C,D 四点共圆,可得∠ABC=∠CDF,AB=AC可得∠ABC=∠ACB,从而得解.
(II)证明△BAD∽△FAB,可得AB2=AD•AF,因为AB=AC,所以AB•AC=AD•AF,再根据割线定理即可得到结论.
解答 证明:(I)∵A,B,C,D 四点共圆,∴∠ABC=∠CDF
又AB=AC∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,
对顶角∠EDF=∠ADB,故∠EDF=∠CDF;
(II)由(I)得∠ADB=∠ABF,
∵∠BAD=∠FAB,
∴△BAD∽△FAB,
∴$\frac{AB}{AF}$=$\frac{AD}{AB}$,
∴AB2=AD•AF,
∵AB=AC,
∴AB•AC=AD•AF,
∴AB•AC•DF=AD•AF•DF,
根据割线定理DF•AF=FC•FB,
∴AB•AC•DF=AD•FC•FB.
点评 本题以圆为载体,考查圆的内接四边形的性质,考查等腰三角形的性质,考查三角形的相似,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图所示,AB为圆O的直径,BC为圆O的切线,B为切点,D为圆O上一点,AD∥OC.
如图所示,AB为圆O的直径,BC为圆O的切线,B为切点,D为圆O上一点,AD∥OC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}π$ | B. | $\frac{2}{3}π$ | C. | -$\frac{5}{6}π$ | D. | $\frac{5}{6}π$ |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:填空题
已知三次函数 ,下列命题正确的是 .
,下列命题正确的是 .
①函数 关于原点
关于原点 中心对称;
中心对称;
②以 ,
, 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与 交于
交于 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系 ;
;
③以 为切点,作切线与
为切点,作切线与 图像交于点
图像交于点 ,再以点
,再以点 为切点作直线与
为切点作直线与 图像交于点
图像交于点 ,再以点
,再以点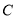 作切点作直线与
作切点作直线与 图像交于点
图像交于点 ,则
,则 点横坐标为
点横坐标为 ;
;
④若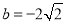 ,函数
,函数 图像上存在四点
图像上存在四点 ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:解答题
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中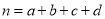 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com